Koska logaritmien kantaluvut ovat yhtä suuret. Edellytykset logaritmin määrittämiselle. Logaritmikaavojen käyttäminen: Esimerkkejä ja ratkaisuja

Logaritmin määritelmä

Luvun b logaritmi kantaan a on eksponentti, johon sinun on nostettava a saadaksesi b.

Numero e matematiikassa on tapana merkitä raja, johon lauseke pyrkii

Numero e on irrationaalinen luku- numero, joka on epäsuhtainen yhteen, sitä ei voida ilmaista tarkasti kokonaisuutena tai murto-osana järkevää määrä.

Kirje e- latinalaisen sanan ensimmäinen kirjain exonere- kehua, tästä nimi matematiikassa eksponentiaalinen- eksponentti funktio.

Määrä e käytetään laajalti matematiikassa ja kaikissa tieteissä, tavalla tai toisella käyttäen matemaattisia laskelmia tarpeisiinsa.

Logaritmit. Logaritmien ominaisuudet

Määritelmä: Positiivisen luvun b kantalogaritmi on eksponentti c, johon luku a on nostettava luvun b saamiseksi.

Logaritmisen perusidentiteetti:

7) Kaava uuteen tukikohtaan siirtymiselle:

lna = log e a, e ≈ 2,718…

Tehtävät ja testit aiheesta "Logaritmit. Logaritmien ominaisuudet»

• Logaritmit - Tärkeitä aiheita matematiikan kokeen toistamiseen

varten onnistunut toteutus tehtävät tästä aiheesta Sinun tulee tietää logaritmin määritelmä, logaritmien ominaisuudet, logaritmisen perusidentiteetti, desimaali- ja luonnollislogaritmien määritelmät. Tämän aiheen pääasialliset tehtävätyypit ovat logaritmisten lausekkeiden laskenta- ja muunnostehtävät. Tarkastellaan heidän ratkaisuaan seuraavissa esimerkeissä.

Ratkaisu: Käyttämällä logaritmien ominaisuuksia saamme

Ratkaisu: käyttämällä asteen ominaisuuksia, saamme

1) (2 2) log 2 5 =(2 log 2 5) 2 = 5 2 =25

Logaritmien, formulaatioiden ja todisteiden ominaisuudet.

Logaritmeilla on useita tunnusomaisia ​​ominaisuuksia. Tässä artikkelissa analysoimme tärkeimmät logaritmien ominaisuudet. Täällä annamme niiden formulaatiot, kirjoitamme logaritmien ominaisuudet kaavojen muodossa, näytämme esimerkkejä niiden soveltamisesta ja annamme myös todisteita logaritmien ominaisuuksista.

Sivulla navigointi.

Logaritmien perusominaisuudet, kaavat

Muistamisen ja käytön helpottamiseksi esittelemme logaritmien perusominaisuudet kaavojen luettelona. Seuraavassa osiossa annamme niiden muotoilut, todisteet, käyttöesimerkit ja tarvittavat selitykset.

Yksikön lokiominaisuus: log a 1=0 mille tahansa a>0 , a≠1 .

Luvun logaritmi, joka on yhtä suuri kuin kanta: loga a a=1, jos a>0 , a≠1 .

Kantaasteen logaritmin ominaisuus: log a a p =p , missä a>0 , a≠1 ja p on mikä tahansa oikea numero.

Kahden positiivisen luvun tulon logaritmi: log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
ja n positiivisen luvun tulon logaritmin ominaisuus: log a (x 1 x 2 ... xn) = log ax 1 + log ax 2 + ... + log axn, a>0, a≠1, x 1 >0, x 2 >0, …, xn >0.

Yksityinen logaritmiominaisuus: , jossa a>0, a≠1, x>0, y>0.

Luvun potenssin logaritmi: log a b p =p log a |b| , jossa a>0, a≠1, b ja p ovat sellaisia ​​lukuja, että b p:n aste on järkevä ja b p >0.

Seuraus: , jossa a>0, a≠1, n – luonnollinen luku, suurempi kuin yksi, b>0.

Seuraus 1: , a>0, a≠1, b>0, b≠1.

Seuraus 2: , a>0 , a≠1 , b>0 , p ja q ovat reaalilukuja, q≠0 , erityisesti kun b=a meillä on .

Kiinteistöjen lausunnot ja todisteet

Siirrymme logaritmien tallennettujen ominaisuuksien muotoiluun ja todistamiseen. Kaikki logaritmien ominaisuudet todistetaan logaritmin määritelmän ja siitä seuraavan logaritmisen perusidentiteetin sekä asteen ominaisuuksien perusteella.

Aloitetaan ykseyden logaritmin ominaisuudet. Sen muotoilu on seuraava: yksikön logaritmi on yhtä suuri kuin nolla, eli log a 1=0 mille tahansa a>0, a≠1. Todistus on suoraviivainen: koska a 0 =1 mille tahansa a:lle, joka täyttää yllä olevat ehdot a>0 ja a≠1 , niin todistettu yhtäläisyys log a 1=0 seuraa välittömästi logaritmin määritelmästä.

Otetaan esimerkkejä tarkasteltavan ominaisuuden soveltamisesta: log 3 1=0 , lg1=0 ja .

Siirrytään seuraavaan omaisuuteen: kantaa vastaavan luvun logaritmi on yhtä suuri kuin yksi, tuo on, log a a=1 jos a>0, a≠1. Todellakin, koska a 1 =a mille tahansa a:lle, niin logaritmin määritelmän mukaan log a a=1 .

Esimerkkejä tämän logaritmien ominaisuuden käytöstä ovat log 5 5=1 , log 5.6 5.6 ja lne=1 .

Logaritmin kantaa vastaavan luvun potenssin logaritmi on yhtä suuri kuin eksponentti. Tämä logaritmin ominaisuus vastaa muodon kaavaa log a a p =p, jossa a>0, a≠1 ja p on mikä tahansa reaaliluku. Tämä ominaisuus seuraa suoraan logaritmin määritelmästä. Huomaa, että sen avulla voit määrittää heti logaritmin arvon, jos logaritmin merkin alla oleva luku on mahdollista esittää kanta-asteena, puhumme tästä lisää logaritmien laskentaa käsittelevässä artikkelissa.

Esimerkiksi log 2 2 7 =7, log10 -4 =-4 ja .

Kahden positiivisen luvun tulon logaritmi x ja y on yhtä suuri kuin näiden lukujen logaritmien tulo: log a (x y)=log a x+log a y, a>0, a≠1. Todistakaamme tuotteen logaritmin ominaisuus. Asteen ominaisuuksista johtuen log ax + log ay =a log ax a log ay, ja koska päälogaritmisen identiteetin mukaan log ax =x ja log ay =y , niin log ax a log ay =x y . Siten log a x+log a y =x y , josta logaritmin määritelmä seuraa vaadittua yhtälöä.

Otetaan esimerkkejä tuotteen logaritmin ominaisuuden käytöstä: log 5 (2 3)=log 5 2+log 5 3 ja .

Tulon logaritmin ominaisuus voidaan yleistää positiivisten lukujen x 1 , x 2 , …, x n äärellisen luvun n tuloksi. log a (x 1 x 2 ... x n)= log a x 1 +log a x 2 +...+log a x n. Tämä yhtäläisyys voidaan helposti todistaa matemaattisen induktion menetelmällä.

Esimerkiksi tuotteen luonnollinen logaritmi voidaan korvata lukujen 4, e ja kolmen luonnollisen logaritmin summalla.

Kahden positiivisen luvun osamäärän logaritmi x ja y on yhtä suuri kuin näiden lukujen logaritmien välinen ero. Osamäärälogaritmin ominaisuus vastaa muodon kaavaa , jossa a>0, a≠1, x ja y ovat joitain positiivisia lukuja. Tämän kaavan pätevyys todistetaan kuten tuotteen logaritmin kaava: koska , sitten logaritmin määritelmän mukaan .

Tässä on esimerkki tämän logaritmin ominaisuuden käyttämisestä: .

Jatketaan asteen logaritmin ominaisuus. Asteen logaritmi on yhtä suuri kuin eksponentin ja tämän asteen kantamoduulin logaritmi. Kirjoitamme tämän asteen logaritmin ominaisuuden kaavan muodossa: log a b p =p log a |b|, jossa a>0, a≠1, b ja p ovat sellaisia ​​lukuja, että b p:n aste on järkevä ja b p >0.

Todistamme ensin tämän ominaisuuden positiiviselle b:lle. Logaritmisen perusidentiteetin avulla voimme esittää luvun b muodossa log a b , jolloin b p =(a log a b) p , ja tuloksena oleva lauseke on potenssiominaisuudesta johtuen yhtä suuri kuin a p log a b . Joten päästään yhtälöön b p =a p log a b , josta logaritmin määritelmän perusteella päätellään, että log a b p =p log a b .

On vielä todistettava tämä ominaisuus negatiiviselle b:lle. Tässä huomautetaan, että lauseke log a b p negatiiviselle b:lle on järkevä vain parillisille eksponenteille p (koska asteen b p arvon on oltava suurempi kuin nolla, muuten logaritmissa ei ole järkeä), ja tässä tapauksessa b p =|b| p . Sitten b p =|b| p =(a log a |b|) p =a p log a |b| , josta log a b p =p log a |b| .

Esimerkiksi, ja ln(-3)4 =4 ln|-3|=4 ln3.

Se seuraa edellisestä omaisuudesta logaritmin ominaisuus juuresta: n:nnen asteen juuren logaritmi on yhtä suuri kuin murtoluvun 1/n ja juurilausekkeen logaritmin tulo, eli missä a>0, a≠1, n on yhtä suurempi luonnollinen luku, b>0.

Todistus perustuu yhtälöön (katso eksponentin määritelmä murto-eksponentilla), joka pätee mille tahansa positiiviselle b:lle, ja asteen logaritmin ominaisuuteen: .

Tässä on esimerkki tämän ominaisuuden käytöstä: .

Nyt todistetaan muunnoskaava logaritmin uuteen kantaan ystävällinen . Tätä varten riittää, kun todistetaan yhtälön log c b=log a b log c a pätevyys. Logaritmisen perusidentiteetin avulla voimme esittää luvun b muodossa log a b, sitten log c b=log c a log a b . Jäljelle jää käyttää asteen logaritmin ominaisuutta: log c a log a b = log a b log c a . Siten yhtälö log c b=log a b log c a on todistettu, mikä tarkoittaa, että myös logaritmin uuteen kantaan siirtymisen kaava on todistettu .

Otetaan pari esimerkkiä tämän logaritmien ominaisuuden soveltamisesta: ja .

Uuteen kantaan siirtymisen kaavan avulla voit siirtyä työskentelemään logaritmien kanssa, joilla on "kätevä" kanta. Sen avulla voidaan esimerkiksi vaihtaa luonnollisiin tai desimaalilogaritmiin, jotta voit laskea logaritmin arvon logaritmitaulukosta. Uuteen logaritmin kantaan siirtymisen kaava mahdollistaa myös joissain tapauksissa tietyn logaritmin arvon löytämisen, kun joidenkin logaritmien arvot muilla kantaluvuilla ovat tiedossa.

Usein käytetään erikoistapausta siirtymäkaavasta logaritmin uuteen kantaan muodon c=b:lle. Tämä osoittaa, että log a b ja log b a ovat keskenään käänteisiä lukuja. Esimerkiksi, .

Kaavaa käytetään myös usein, mikä on kätevää logaritmiarvojen etsimisessä. Sanojemme vahvistamiseksi näytämme kuinka lomakkeen logaritmin arvo lasketaan sen avulla. Meillä on . Kaavan todistamiseksi riittää, kun käytetään siirtymäkaavaa logaritmin a uuteen kantaan: .

On vielä todistettava logaritmien vertailuominaisuudet.

Käytetään päinvastaista menetelmää. Oletetaan, että a 1 >1, a 2 >1 ja a 1 2 ja 0 1 log a 1 b≤log a 2 b on totta. Logaritmien ominaisuuksien perusteella nämä epäyhtälöt voidaan kirjoittaa uudelleen muotoon ja vastaavasti, ja niistä seuraa, että log b a 1 ≤log b a 2 ja log b a 1 ≥ log b a 2, vastaavasti. Tällöin samoilla kantakantoilla olevien potenssien ominaisuuksien perusteella yhtäläisyydet b log b a 1 ≥b log b a 2 ja b log b a 1 ≥b log b a 2 on täytettävä, eli a 1 ≥a 2 . Siten olemme päätyneet ristiriidaan ehdon a 1 2 kanssa. Tämä täydentää todistuksen.

Logaritmien perusominaisuudet

• Materiaalit oppitunnille
• Lataa kaikki kaavat

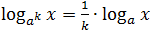
Logaritmeja, kuten mitä tahansa lukua, voidaan lisätä, vähentää ja muuntaa kaikin mahdollisin tavoin. Mutta koska logaritmit eivät ole aivan tavallisia lukuja, tässä on säännöt, joita kutsutaan perusominaisuudet.

Nämä säännöt on tunnettava - ilman niitä ei voida ratkaista vakavaa logaritmista ongelmaa. Lisäksi niitä on hyvin vähän - kaikki voidaan oppia yhdessä päivässä. Joten aloitetaan.

Logaritmien yhteen- ja vähennyslasku

Tarkastellaan kahta logaritmia, joilla on sama kanta: log a x ja log a y . Sitten ne voidaan lisätä ja vähentää, ja:

Joten logaritmien summa on yhtä suuri kuin tuotteen logaritmi, ja ero on osamäärän logaritmi. Huomaa: avainkohta tässä on - samoilla perusteilla. Jos perusteet ovat erilaiset, nämä säännöt eivät toimi!

Nämä kaavat auttavat laskemaan logaritmisen lausekkeen, vaikka sen yksittäisiä osia ei otettaisi huomioon (katso oppitunti "Mikä on logaritmi"). Katso esimerkkejä - ja katso:

Tehtävä. Etsi lausekkeen arvo: log 6 4 + log 6 9.

Koska logaritmien kantaluvut ovat samat, käytämme summakaavaa:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Tehtävä. Etsi lausekkeen arvo: log 2 48 − log 2 3.

Perusteet ovat samat, käytämme erokaavaa:
log 2 48 - log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Tehtävä. Etsi lausekkeen arvo: log 3 135 − log 3 5.

Jälleen, perusteet ovat samat, joten meillä on:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Kuten näet, alkuperäiset lausekkeet koostuvat "huonoista" logaritmeista, joita ei käsitellä erikseen. Mutta muunnosten jälkeen tulee melko normaaleja lukuja. Tämän tosiasian perusteella monet koepaperit. Kyllä, sitä kontrollia - samanlaisia ​​ilmaisuja täysin vakavissaan (joskus - käytännössä ilman muutoksia) tarjotaan kokeessa.

Eksponentin poistaminen logaritmista

Monimutkaistaan ​​nyt tehtävää hieman. Entä jos logaritmin kantaosassa tai argumentissa on aste? Sitten tämän asteen eksponentti voidaan ottaa pois logaritmin etumerkistä seuraavien sääntöjen mukaisesti:

• log a x n = n log a x ;
• 
• 

On helppo nähdä, että viimeinen sääntö seuraa heidän kahta ensimmäistä. Mutta on parempi muistaa se joka tapauksessa - joissain tapauksissa se vähentää merkittävästi laskelmien määrää.

Tietysti kaikki nämä säännöt ovat järkeviä, jos ODZ-logaritmia noudatetaan: a > 0, a ≠ 1, x > 0. Ja vielä yksi asia: opi soveltamaan kaikkia kaavoja paitsi vasemmalta oikealle, myös päinvastoin, ts. voit syöttää logaritmin etumerkkiä edeltävät luvut itse logaritmiin. Tätä vaaditaan useimmiten.

Tehtävä. Etsi lausekkeen arvo: log 7 49 6 .

Päästään eroon argumentin asteesta ensimmäisen kaavan mukaan:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Tehtävä. Etsi lausekkeen arvo:

[Kuvan kuvateksti]

Huomaa, että nimittäjä on logaritmi, jonka kanta ja argumentti ovat tarkat potenssit: 16 = 2 4 ; 49 = 72. Meillä on:

[Kuvan kuvateksti]

Mielestäni viimeinen esimerkki kaipaa selvennystä. Mihin logaritmit ovat kadonneet? Viimeiseen hetkeen asti työskentelemme vain nimittäjällä. He esittivät siellä seisovan logaritmin kannan ja argumentin asteiden muodossa ja ottivat indikaattorit - he saivat "kolmikerroksisen" murto-osan.

Katsotaan nyt pääosaa. Osoittajalla ja nimittäjällä on sama luku: log 2 7. Koska log 2 7 ≠ 0, voimme pienentää murto-osaa - 2/4 jää nimittäjään. Aritmeettisten sääntöjen mukaan neljä voidaan siirtää osoittajaan, mikä tehtiin. Tuloksena on vastaus: 2.

Siirtyminen uudelle perustalle

Puhuessani logaritmien yhteen- ja vähennyssäännöistä korostin erityisesti, että ne toimivat vain samoilla perusteilla. Entä jos pohjat ovat erilaiset? Entä jos ne eivät ole täsmälleen saman luvun potenssit?

Uuteen tukikohtaan siirtymisen kaavat tulevat apuun. Muotoilemme ne lauseen muodossa:

Olkoon logaritmi log a x annettu. Sitten mille tahansa luvulle c, jonka c > 0 ja c ≠ 1, yhtälö on tosi:

[Kuvan kuvateksti]

Erityisesti, jos laitamme c = x , saamme:

[Kuvan kuvateksti]

Toisesta kaavasta seuraa, että logaritmin kanta ja argumentti voidaan vaihtaa keskenään, mutta tässä tapauksessa koko lauseke "käännetään" ts. logaritmi on nimittäjässä.

Näitä kaavoja löytyy harvoin tavallisista numeerisia lausekkeita. On mahdollista arvioida, kuinka käteviä ne ovat, vasta päätettäessä logaritmiset yhtälöt ja eriarvoisuudet.

On kuitenkin tehtäviä, joita ei voida ratkaista ollenkaan muutoin kuin siirtymällä uudelle perustalle. Tarkastellaanpa paria näistä:

Tehtävä. Etsi lausekkeen arvo: log 5 16 log 2 25.

Huomaa, että molempien logaritmien argumentit ovat tarkat eksponentit. Otetaan indikaattorit pois: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2 log 2 5;

Käännetään nyt toinen logaritmi:

[Kuvan kuvateksti]

Koska tulo ei muutu tekijöiden permutaatiosta, kerroimme rauhallisesti neljä ja kaksi ja sitten selvitimme logaritmit.

Tehtävä. Etsi lausekkeen arvo: log 9 100 lg 3.

Ensimmäisen logaritmin kanta ja argumentti ovat tarkat potenssit. Kirjataan se ylös ja päästään eroon indikaattoreista:

[Kuvan kuvateksti]

Nyt päästään eroon desimaalilogaritmi, muuttaminen uuteen tukikohtaan:

[Kuvan kuvateksti]

Peruslogaritminen identiteetti

Usein ratkaisuprosessissa on esitettävä luku logaritmina tiettyyn kantaan. Tässä tapauksessa kaavat auttavat meitä:

1. n = log a a n

2. Ensimmäisessä tapauksessa luvusta n tulee argumentin eksponentti. Luku n voi olla mitä tahansa, koska se on vain logaritmin arvo.

   Toinen kaava on itse asiassa parafrasoitu määritelmä. Sitä kutsutaan logaritmiseksi perusidentiteetiksi.

   Todellakin, mitä tapahtuu, jos luku b nostetaan niin suureen potenssiin, että luku b tähän potenssiin antaa luvun a? Aivan oikein: tämä on sama numero a . Lue tämä kappale huolellisesti uudelleen - monet ihmiset "roikkuvat" siinä.

   Kuten uudet perusmuunnoskaavat, logaritminen perusidentiteetti on joskus ainoa mahdollinen ratkaisu.

   [Kuvan kuvateksti]

   Huomaa, että log 25 64 = log 5 8 - ota vain kantaluvun neliö ja logaritmin argumentti. Ottaen huomioon potenssien kertomisen säännöt samalla kantalla, saamme:

   [Kuvan kuvateksti]

   Jos joku ei ole perillä, tämä oli oikea tehtävä yhtenäisestä valtiokokeesta 🙂

   Logaritminen yksikkö ja logaritminen nolla

   Lopuksi annan kaksi identiteettiä, joita on vaikea kutsua ominaisuuksiksi - pikemminkin nämä ovat seurauksia logaritmin määritelmästä. Heitä löytyy jatkuvasti ongelmista ja yllättäen ne aiheuttavat ongelmia jopa "edenneille" opiskelijoille.

   1. log a a = 1 on logaritminen yksikkö. Muista kerta kaikkiaan: logaritmi mihin tahansa kantaan a itse tästä kannasta on yhtä suuri kuin yksi.
   2. log a 1 = 0 on logaritminen nolla. Kanta a voi olla mikä tahansa, mutta jos argumentti on yksi - logaritmi on nolla! Koska 0 = 1 on määritelmän suora seuraus.

   Siinä kaikki ominaisuudet. Muista harjoitella niiden toteuttamista käytännössä! Lataa huijauslehti oppitunnin alussa, tulosta se - ja ratkaise ongelmat.

   Logaritmi. Logaritmin ominaisuudet (yhteen- ja vähennyslasku).

   Logaritmin ominaisuudet seuraa sen määritelmästä. Ja niin luvun logaritmi b syystä a määritellään eksponenttiksi, johon luku on nostettava a saadaksesi numeron b(logaritmi on olemassa vain positiivisille luvuille).

   Tästä sanamuodosta seuraa, että laskelma x=log a b, vastaa yhtälön ratkaisemista ax=b. Esimerkiksi, log 2 8 = 3 koska 8 = 2 3 . Logaritmin muotoilu mahdollistaa sen, että jos b=a c, sitten luvun logaritmi b syystä a on yhtä suuri Kanssa. On myös selvää, että logaritmin aihe liittyy läheisesti luvun potenssiin.

   Logaritmeilla, kuten millä tahansa numerolla, voit suorittaa yhteen- ja vähennysoperaatiot ja muuttaa kaikin mahdollisin tavoin. Mutta koska logaritmit eivät ole aivan tavallisia lukuja, tässä pätevät omat erityissäännönsä, joita kutsutaan ns. perusominaisuudet.

   Logaritmien yhteen- ja vähennyslasku.

   Ota kaksi logaritmia samalla kantavalla: loki x ja kirjaudu a y. Poista sitten on mahdollista suorittaa yhteen- ja vähennystoimintoja:

   Kuten näemme, logaritmien summa on yhtä suuri kuin tulon logaritmi ja ero logaritmit- osamäärän logaritmi. Ja tämä on totta, jos numerot a, X ja klo positiivinen ja a ≠ 1.

   On tärkeää huomata, että näiden kaavojen pääasialliset perusteet ovat samat. Jos pohjat eroavat toisistaan, nämä säännöt eivät päde!

   Saman kantavuuden logaritmien yhteen- ja vähennyssääntöjä luetaan paitsi vasemmalta oikealle, myös päinvastoin. Tämän seurauksena meillä on lauseet tulon logaritmille ja osamäärän logaritmille.

   Tuotteen logaritmi kaksi positiivista numeroa on yhtä suuri kuin summa niiden logaritmit ; parafrasoidaan tämä lause, saamme seuraavan, jos numerot a, x ja klo positiivinen ja a ≠ 1, sitten:

   Osamäärän logaritmi kahden positiivisen luvun välinen ero on yhtä suuri kuin osingon ja jakajan logaritmien välinen ero. Toisin sanoen, jos numerot a, X ja klo positiivinen ja a ≠ 1, sitten:

   Käytämme yllä olevia lauseita ratkaisemaan esimerkkejä:

   Jos numeroita x ja klo ovat sitten negatiivisia tuotteen logaritmikaava muuttuu merkityksettömäksi. Joten on kiellettyä kirjoittaa:

   koska lausekkeita log 2 (-8) ja log 2 (-4) ei ole määritelty ollenkaan (logaritminen funktio klo= loki 2 X määritelty vain positiiviset arvot Perustelu X).

   Tuotelause ei sovelleta vain kahteen, vaan myös rajoittamattomaan määrään tekijöitä. Tämä tarkoittaa, että jokaiselle luonnolliselle k ja mahdolliset positiiviset luvut x 1 , x 2 , . . . ,x n on identiteetti:

   From osamäärä logaritmilauseet voidaan saada yksi logaritmin ominaisuus lisää. Se loki on hyvin tiedossa a 1 = 0, joten

   Eli tasa-arvo on olemassa:

   Kahden keskenään käänteisen luvun logaritmit samalla perusteella eroavat toisistaan ​​vain merkillä. Niin:

   Logaritmi. Logaritmien ominaisuudet

   Logaritmi. Logaritmien ominaisuudet

   Harkitse tasa-arvoa. Kerro meille arvot ja haluamme löytää arvon.

   Eli etsimme eksponenttia, johon sinun täytyy kukko päästä.

   Päästää muuttuja voi ottaa minkä tahansa todellisen arvon, niin muuttujille asetetaan seuraavat rajoitukset: o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/ >

   Jos tiedämme ja arvot ja edessämme on tehtävä löytää tuntematon, niin tätä tarkoitusta varten otetaan käyttöön matemaattinen operaatio, joka on ns. logaritmi.

   Löytääksemme saamamme arvon luvun logaritmi päällä perusta :

   Luvun logaritmi kantaan on eksponentti, johon sinun on nostettava saadaksesi .

   Tuo on logaritminen perusidentiteetti:

   o” title=”a>o”/> , 1” title=”a1″/>, 0” title=”b>0”/>

   on pohjimmiltaan matemaattinen merkintä logaritmin määritelmät.

   Matemaattinen operaatiologaritmi on eksponentioimisen käänteinen, joten logaritmien ominaisuudet liittyvät läheisesti tutkinnon ominaisuuksiin.

   Luettelemme tärkeimmät logaritmien ominaisuudet:

   (o” title=”a>o”/> , 1” title=”a1″/>, 0” title=”b>0”/>, 0,

   d>0″/>, 1″ title=”d1″/>

   4.

   5.

   Seuraavan ominaisuusryhmän avulla voit esittää lausekkeen eksponentin logaritmin etumerkin alla tai logaritmin pohjalla olevana kertoimena ennen logaritmin etumerkkiä:

   6.

   7.

   8.

   9.

   Seuraava kaavaryhmä mahdollistaa siirtymisen logaritmista, jolla on annettu kanta, logaritmiin, jossa on mielivaltainen kanta, ja sitä kutsutaan siirtymäkaavat uuteen kantaan:

   10.

   12. (seuraus omaisuudesta 11)

   

   Seuraavat kolme ominaisuutta eivät ole hyvin tunnettuja, mutta niitä käytetään usein ratkattaessa logaritmisia yhtälöitä tai yksinkertaistettaessa logaritmeja sisältäviä lausekkeita:

   13.

   14.

   15.

   Erikoistapaukset:

   — desimaalilogaritmi

   — luonnollinen logaritmi

   Yksinkertaistettaessa logaritmeja sisältäviä lausekkeita käytetään yleistä lähestymistapaa:

   1. Esittelyssä desimaalit tavallisen muodossa.

   2. Esitämme sekaluvut virheellisinä murtolukuina.

   3. Logaritmin kantapään ja logaritmin etumerkin alla olevat luvut jaetaan alkutekijöiksi.

   4. Yritämme saada kaikki logaritmit samalle kantalle.

   5. Käytä logaritmien ominaisuuksia.

   Katsotaanpa esimerkkejä logaritmeja sisältävien lausekkeiden yksinkertaistamisesta.

   Esimerkki 1

   Laskea:

   Yksinkertaistetaan kaikki eksponentit: tehtävämme on saattaa ne logaritmeihin, joiden kanta on sama kuin eksponentin kanta.

   ==(ominaisuuden 7 mukaan)=(ominaisuuden 6 mukaan) =

   Korvaa alkuperäisessä lausekkeessa saamamme indikaattorit. Saamme:

   Vastaus: 5.25

   Esimerkki 2 Laske:

   

   Tuomme kaikki logaritmit kantaan 6 (tässä tapauksessa logaritmit murtoluvun nimittäjästä "siirtyvät" osoittajaan):

   Jaetaan logaritmin etumerkin alla olevat luvut alkutekijöiksi:

   Käytä ominaisuuksia 4 ja 6:

   Esittelemme korvaavan

   Saamme:

   Vastaus: 1

   Logaritmi . Peruslogaritminen identiteetti.

   Logaritmien ominaisuudet. Desimaalilogaritmi. luonnollinen logaritmi.

   logaritmi positiivinen luku N kantaosassa (b > 0, b 1) kutsutaan eksponenttiksi x, johon sinun on nostettava b saadaksesi N .

   Tämä merkintä vastaa seuraavaa: b x = N .

   ESIMERKKEJÄ: log 3 81 = 4 koska 3 4 = 81 ;

   log 1/3 27 = – 3, koska (1/3) - 3 = 3 3 = 27 .

   Yllä oleva logaritmin määritelmä voidaan kirjoittaa identiteetiksi:

   

   Logaritmien perusominaisuudet.

   2) log 1 = 0, koska b 0 = 1 .

   3) Tuloksen logaritmi on yhtä suuri kuin tekijöiden logaritmien summa:

   4) Osamäärän logaritmi on yhtä suuri kuin osingon ja jakajan logaritmien välinen ero:

   5) Asteen logaritmi on yhtä suuri kuin eksponentin ja sen kantaluvun logaritmi:

   Tämän ominaisuuden seuraus on seuraava: lokijuuri on yhtä suuri kuin juuriluvun logaritmi jaettuna juuren potenssilla:

   

   6) Jos logaritmin kanta on aste, niin arvo eksponentin käänteisluku voidaan ottaa pois riimilokimerkistä:

   

   Kaksi viimeistä ominaisuutta voidaan yhdistää yhdeksi:

   

   7) Siirtymämoduulin kaava (eli siirtyminen logaritmin yhdestä kannasta toiseen):

   

   Tietyssä tapauksessa, milloin N = a meillä on:

   

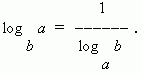
   Desimaalilogaritmi olla nimeltään peruslogaritmi 10. Sitä merkitään lg:llä, ts. loki 10 N= loki N. Lukujen 10, 100, 1000, . p ovat 1, 2, 3, …, vastaavasti, ts. on niin paljon positiivista

   yksikköä, kuinka monta nollaa on logaritmiluvussa yhden jälkeen. Lukujen logaritmit 0,1, 0,01, 0,001, . p ovat vastaavasti –1, –2, –3, …, ts. on yhtä monta negatiivista kuin on nollia logaritmiluvussa ennen yhtä (mukaan lukien nolla kokonaislukua). Jäljellä olevien lukujen logaritmeilla on murto-osa nimeltään mantissa. koko osa kutsutaan logaritmiksi ominaisuus. Käytännön sovelluksissa desimaalilogaritmit ovat kätevimpiä.

   luonnollinen logaritmi olla nimeltään peruslogaritmi e. Sitä merkitään ln:llä, ts. Hirsi e N=ln N. Määrä e on irrationaalinen, sen likimääräinen arvo on 2,718281828. Se on raja, jota kohti numero (1 + 1 / n) n rajoittamattomalla korotuksella n(cm. ensimmäinen ihana raja"Rajat"-sivulla numerosarjat»).
   Niin oudolta kuin se saattaakin tuntua, luonnolliset logaritmit osoittautuivat erittäin käteviksi suoritettaessa erilaisia ​​funktioiden analysointiin liittyviä operaatioita. Peruslogaritmien laskeminen e paljon nopeammin kuin mikään muu perusta.

• Mitä tarvitset tänään adoptoidaksesi lapsen Venäjälle? Adoptio Venäjällä sisältää vastuullisen henkilökohtaisen päätöksen lisäksi useita menettelyjä ehdokkaiden valtion varmentamiseksi. Vaikea valinta valmisteluvaihe edistää enemmän […]
• Maksuton TIN- tai PSRN-tiedot verorekisteristä kaikkialla Venäjällä - verkossa Veropalveluiden yhtenäisportaalissa tietoa valtion rekisteröinti oikeushenkilöitä, yksittäiset yrittäjät, […]
• Rangaistus ilman asiakirjoja ajamisesta ( ajokortti, vakuutus, STS) Joskus unohduksen vuoksi kuljettajat istuvat ratin taakse ilman ajoneuvoa ja saavat sakon ajamisesta ilman asiakirjoja. Muista, että hänen kanssaan ajava autoilija epäonnistui […]
• Kukat miehille. Millaisia ​​kukkia voit antaa miehelle? Mitä kukkia voi antaa miehelle? Ei ole niin paljon "uroskukkia", mutta on niitä, jotka annetaan miehille. Pieni luettelo kukista edessäsi: Krysanteemit. Ruusut. Neilikat. […]
• muistio- se erityinen muoto asiakirjassa, jota käytetään sisäinen ympäristö yritys ja auttaa ratkaisemaan nopeasti nykyiset tuotantoongelmat. Yleensä tämä asiakirja on laadittu jonkin verran […]
• Milloin ja miten saada rahastoitu osa eläkkeestä Sberbankissa? Sberbank on valtion eläkerahaston kumppanipankki. Tämän perusteella rahastoivan eläkkeen myöntäneet kansalaiset voisivat siirtää rahastoivan […]
• Lapsilisät Uljanovskissa ja Uljanovskin alueella vuonna 2018 Lisäksi liittovaltion lain hyväksymät ohjelmat ovat voimassa kaikilla alueilla. Katsotaan, kuka ja mihin etuihin voi luottaa. Miten alueviranomaiset […]
• Yksityiskohtainen opas valtakirjan laatimisesta yksityishenkilön etujen edustamiseksi tuomioistuimessa Siviili- tai välimiesoikeudenkäynnissä, hallinto- tai rikosasiassa sekä kantajan että vastaajan etuja voi edustaa asianajaja: […]

perusominaisuudet.

1. logax + logay = log(x y);
2. logax − logay = log(x: y).

samoilla perusteilla

log6 4 + log6 9.

Monimutkaistaan ​​nyt tehtävää hieman.

Esimerkkejä logaritmien ratkaisemisesta

Entä jos logaritmin kantaosassa tai argumentissa on aste? Sitten tämän asteen eksponentti voidaan ottaa pois logaritmin etumerkistä seuraavien sääntöjen mukaisesti:

Tietenkin kaikki nämä säännöt ovat järkeviä, jos ODZ-logaritmia noudatetaan: a > 0, a ≠ 1, x >

Tehtävä. Etsi lausekkeen arvo:

Siirtyminen uudelle perustalle

Olkoon logaritmin logaksi annettu. Sitten mille tahansa luvulle c, jonka c > 0 ja c ≠ 1, yhtälö on tosi:

Tehtävä. Etsi lausekkeen arvo:

Katso myös:

Logaritmin perusominaisuudet

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

Eksponentti on 2,718281828…. Eksponentin muistamiseksi voit tutkia sääntöä: eksponentti on 2,7 ja kaksi kertaa Leo Tolstoin syntymävuosi.

Logaritmien perusominaisuudet

Kun tiedät tämän säännön, tiedät ja tarkka arvo näytteilleasettajat ja Leo Tolstoin syntymäaika.

Esimerkkejä logaritmeista

Ota lausekkeiden logaritmi

Esimerkki 1
a). x = 10ac^2 (a>0, c>0).

Ominaisuuksilla 3,5 lasketaan

2.

3.

4. missä .

Esimerkki 2 Etsi x jos

Esimerkki 3. Annetaan logaritmien arvot

Laske log(x), jos

Logaritmien perusominaisuudet

Logaritmeja, kuten mitä tahansa lukua, voidaan lisätä, vähentää ja muuntaa kaikin mahdollisin tavoin. Mutta koska logaritmit eivät ole aivan tavallisia lukuja, tässä on säännöt, joita kutsutaan perusominaisuudet.

Nämä säännöt on tunnettava - ilman niitä ei voida ratkaista vakavaa logaritmista ongelmaa. Lisäksi niitä on hyvin vähän - kaikki voidaan oppia yhdessä päivässä. Joten aloitetaan.

Logaritmien yhteen- ja vähennyslasku

Tarkastellaan kahta logaritmia, joilla on sama kanta: logaksi ja logarit. Sitten ne voidaan lisätä ja vähentää, ja:

1. logax + logay = log(x y);
2. logax − logay = log(x: y).

Joten logaritmien summa on yhtä suuri kuin tuotteen logaritmi, ja ero on osamäärän logaritmi. Huomaa: avainkohta tässä on - samoilla perusteilla. Jos perusteet ovat erilaiset, nämä säännöt eivät toimi!

Nämä kaavat auttavat laskemaan logaritmisen lausekkeen, vaikka sen yksittäisiä osia ei otettaisi huomioon (katso oppitunti "Mikä on logaritmi"). Katso esimerkkejä ja katso:

Koska logaritmien kantaluvut ovat samat, käytämme summakaavaa:
log6 4 + log6 9 = log6 (4 9) = log6 36 = 2.

Tehtävä. Etsi lausekkeen arvo: log2 48 − log2 3.

Perusteet ovat samat, käytämme erokaavaa:
log2 48 − log2 3 = log2 (48: 3) = log2 16 = 4.

Tehtävä. Etsi lausekkeen arvo: log3 135 − log3 5.

Jälleen, perusteet ovat samat, joten meillä on:
log3 135 − log3 5 = log3 (135: 5) = log3 27 = 3.

Kuten näet, alkuperäiset lausekkeet koostuvat "huonoista" logaritmeista, joita ei käsitellä erikseen. Mutta muunnosten jälkeen tulee melko normaaleja lukuja. Monet testit perustuvat tähän tosiasiaan. Kyllä, kontrolli - samanlaisia ​​ilmaisuja kaikessa vakavuudessa (joskus - käytännössä ilman muutoksia) tarjotaan kokeessa.

Eksponentin poistaminen logaritmista

On helppo nähdä, että viimeinen sääntö seuraa heidän kahta ensimmäistä. Mutta on parempi muistaa se joka tapauksessa - joissain tapauksissa se vähentää merkittävästi laskelmien määrää.

Tietysti kaikki nämä säännöt ovat järkeviä, jos ODZ-logaritmia noudatetaan: a > 0, a ≠ 1, x > 0. Ja vielä yksi asia: opi soveltamaan kaikkia kaavoja paitsi vasemmalta oikealle, myös päinvastoin, ts. voit syöttää logaritmin etumerkkiä edeltävät luvut itse logaritmiin. Tätä vaaditaan useimmiten.

Tehtävä. Etsi lausekkeen arvo: log7 496.

Päästään eroon argumentin asteesta ensimmäisen kaavan mukaan:
log7 496 = 6 log7 49 = 6 2 = 12

Tehtävä. Etsi lausekkeen arvo:

Huomaa, että nimittäjä on logaritmi, jonka kanta ja argumentti ovat tarkat potenssit: 16 = 24; 49 = 72. Meillä on:

Mielestäni viimeinen esimerkki kaipaa selvennystä. Mihin logaritmit ovat kadonneet? Viimeiseen hetkeen asti työskentelemme vain nimittäjällä.

Logaritmien kaavat. Logaritmit ovat esimerkkejä ratkaisuista.

He esittivät siellä seisovan logaritmin kannan ja argumentin asteiden muodossa ja ottivat indikaattorit - he saivat "kolmikerroksisen" murto-osan.

Katsotaan nyt pääosaa. Osoittajalla ja nimittäjällä on sama luku: log2 7. Koska log2 7 ≠ 0, voimme pienentää murto-osaa - 2/4 jää nimittäjään. Aritmeettisten sääntöjen mukaan neljä voidaan siirtää osoittajaan, mikä tehtiin. Tuloksena on vastaus: 2.

Siirtyminen uudelle perustalle

Puhuessani logaritmien yhteen- ja vähennyssäännöistä korostin erityisesti, että ne toimivat vain samoilla perusteilla. Entä jos pohjat ovat erilaiset? Entä jos ne eivät ole täsmälleen saman luvun potenssit?

Uuteen tukikohtaan siirtymisen kaavat tulevat apuun. Muotoilemme ne lauseen muodossa:

Olkoon logaritmin logaksi annettu. Sitten mille tahansa luvulle c, jonka c > 0 ja c ≠ 1, yhtälö on tosi:

Erityisesti, jos laitamme c = x, saamme:

Toisesta kaavasta seuraa, että logaritmin kanta ja argumentti voidaan vaihtaa keskenään, mutta tässä tapauksessa koko lauseke "käännetään" ts. logaritmi on nimittäjässä.

Näitä kaavoja löytyy harvoin tavallisista numeerisista lausekkeista. Niiden käyttökelpoisuutta on mahdollista arvioida vain logaritmiset yhtälöitä ja epäyhtälöitä ratkaistaessa.

On kuitenkin tehtäviä, joita ei voida ratkaista ollenkaan muutoin kuin siirtymällä uudelle perustalle. Tarkastellaanpa paria näistä:

Tehtävä. Etsi lausekkeen arvo: log5 16 log2 25.

Huomaa, että molempien logaritmien argumentit ovat tarkat eksponentit. Otetaan indikaattorit pois: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;

Käännetään nyt toinen logaritmi:

Koska tulo ei muutu tekijöiden permutaatiosta, kerroimme rauhallisesti neljä ja kaksi ja sitten selvitimme logaritmit.

Tehtävä. Etsi lausekkeen arvo: log9 100 lg 3.

Ensimmäisen logaritmin kanta ja argumentti ovat tarkat potenssit. Kirjataan se ylös ja päästään eroon indikaattoreista:

Nyt päästään eroon desimaalilogaritmista siirtymällä uuteen kantaan:

Peruslogaritminen identiteetti

Usein ratkaisuprosessissa on esitettävä luku logaritmina tiettyyn kantaan. Tässä tapauksessa kaavat auttavat meitä:

Ensimmäisessä tapauksessa luvusta n tulee argumentin eksponentti. Luku n voi olla mitä tahansa, koska se on vain logaritmin arvo.

Toinen kaava on itse asiassa parafrasoitu määritelmä. Sitä kutsutaan näin:

Todellakin, mitä tapahtuu, jos lukua b korotetaan siinä määrin, että tämän asteen luku b antaa luvun a? Aivan oikein: tämä on sama numero a. Lue tämä kappale huolellisesti uudelleen - monet ihmiset "roikkuvat" siinä.

Kuten uudet perusmuunnoskaavat, logaritminen perusidentiteetti on joskus ainoa mahdollinen ratkaisu.

Tehtävä. Etsi lausekkeen arvo:

Huomaa, että log25 64 = log5 8 - juuri poisti neliön kannasta ja logaritmin argumentin. Ottaen huomioon potenssien kertomisen säännöt samalla kantalla, saamme:

Jos joku ei ole perillä, tämä oli oikea tehtävä yhtenäisestä valtiokokeesta 🙂

Logaritminen yksikkö ja logaritminen nolla

Lopuksi annan kaksi identiteettiä, joita on vaikea kutsua ominaisuuksiksi - pikemminkin nämä ovat seurauksia logaritmin määritelmästä. Heitä löytyy jatkuvasti ongelmista ja yllättäen ne aiheuttavat ongelmia jopa "edenneille" opiskelijoille.

1. logaa = 1 on. Muista kerta kaikkiaan: logaritmi mihin tahansa kantaan a itse tästä kannasta on yhtä suuri kuin yksi.
2. loga 1 = 0 on. Kanta a voi olla mikä tahansa, mutta jos argumentti on yksi, logaritmi on nolla! Koska a0 = 1 on määritelmän suora seuraus.

Siinä kaikki ominaisuudet. Muista harjoitella niiden toteuttamista käytännössä! Lataa huijauslehti oppitunnin alussa, tulosta se ja ratkaise ongelmat.

Katso myös:

Luvun b logaritmi kantaan a tarkoittaa lauseketta. Logaritmin laskeminen tarkoittaa sellaisen potenssin x () löytämistä, jolla yhtälö on tosi

Logaritmin perusominaisuudet

Yllä olevat ominaisuudet on tunnettava, koska niiden perusteella lähes kaikki tehtävät ja esimerkit ratkaistaan ​​logaritmien perusteella. Loput eksoottiset ominaisuudet voidaan johtaa matemaattisilla manipuloinneilla näillä kaavoilla

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

Laskettaessa kaavoja logaritmien summalle ja erolle (3.4) kohdataan melko usein. Loput ovat melko monimutkaisia, mutta monissa tehtävissä ne ovat välttämättömiä monimutkaisten lausekkeiden yksinkertaistamiseksi ja niiden arvojen laskemiseksi.

Yleisiä logaritmien tapauksia

Jotkut yleisimmistä logaritmeista ovat sellaisia, joissa kanta on jopa kymmenen, eksponentiaalinen tai kakkonen.
Kymmenen kantalogaritmia kutsutaan yleensä kymmenen kantalogaritmiksi ja sitä merkitään yksinkertaisesti lg(x).

Tietueesta näkyy, että perusasiat eivät ole tietueessa kirjoitettuja. Esimerkiksi

Luonnollinen logaritmi on logaritmi, jonka perusta on eksponentti (merkitty ln(x)).

Eksponentti on 2,718281828…. Eksponentin muistamiseksi voit tutkia sääntöä: eksponentti on 2,7 ja kaksi kertaa Leo Tolstoin syntymävuosi. Kun tiedät tämän säännön, tiedät sekä eksponentin tarkan arvon että Leo Tolstoin syntymäajan.

Ja toinen tärkeä kahden peruslogaritmi on

Funktion logaritmin derivaatta on yhtä suuri kuin yksi jaettuna muuttujalla

Integraali tai antideriivatiivinen logaritmi määräytyy riippuvuuden mukaan

Yllä oleva materiaali riittää sinulle ratkaisemaan laajan luokan logaritmeihin ja logaritmeihin liittyviä ongelmia. Aineiston ymmärtämisen vuoksi annan vain muutaman yleisen esimerkin koulun opetussuunnitelma ja yliopistot.

Esimerkkejä logaritmeista

Ota lausekkeiden logaritmi

Esimerkki 1
a). x = 10ac^2 (a>0, c>0).

Ominaisuuksilla 3,5 lasketaan

2.
Logaritmien erotusominaisuudella meillä on

3.
Käyttämällä ominaisuuksia 3.5 löydämme

4. missä .

Ulkonäön perusteella monimutkainen ilmaisu Sääntösarjan käyttäminen on yksinkertaistettu muotoon

Logaritmiarvojen löytäminen

Esimerkki 2 Etsi x jos

Ratkaisu. Laskennassa hyödynnetään ominaisuuksia 5 ja 13 viimeiseen termiin asti

Korvaa pöytäkirjassa ja sure

Koska emäkset ovat yhtä suuret, yhtälöimme lausekkeet

Logaritmit. Ensimmäinen taso.

Olkoon logaritmien arvot annettu

Laske log(x), jos

Ratkaisu: Kirjoita muuttujan logaritmi termien summan läpi

Tämä on vasta alkua logaritmiin ja niiden ominaisuuksiin tutustumiselle. Harjoittele laskelmia, rikasta käytännön taitojasi - tarvitset pian hankittua tietoa logaritmisen yhtälöiden ratkaisemiseen. Tutkittuamme perusmenetelmiä tällaisten yhtälöiden ratkaisemiseksi, laajennamme tietämyksesi toiselle yhtä tärkeälle aiheelle - logaritmisille epäyhtälöille ...

Logaritmien perusominaisuudet

Logaritmeja, kuten mitä tahansa lukua, voidaan lisätä, vähentää ja muuntaa kaikin mahdollisin tavoin. Mutta koska logaritmit eivät ole aivan tavallisia lukuja, tässä on säännöt, joita kutsutaan perusominaisuudet.

Nämä säännöt on tunnettava - ilman niitä ei voida ratkaista vakavaa logaritmista ongelmaa. Lisäksi niitä on hyvin vähän - kaikki voidaan oppia yhdessä päivässä. Joten aloitetaan.

Logaritmien yhteen- ja vähennyslasku

Tarkastellaan kahta logaritmia, joilla on sama kanta: logaksi ja logarit. Sitten ne voidaan lisätä ja vähentää, ja:

1. logax + logay = log(x y);
2. logax − logay = log(x: y).

Joten logaritmien summa on yhtä suuri kuin tuotteen logaritmi, ja ero on osamäärän logaritmi. Huomaa: avainkohta tässä on - samoilla perusteilla. Jos perusteet ovat erilaiset, nämä säännöt eivät toimi!

Nämä kaavat auttavat laskemaan logaritmisen lausekkeen, vaikka sen yksittäisiä osia ei otettaisi huomioon (katso oppitunti "Mikä on logaritmi"). Katso esimerkkejä ja katso:

Tehtävä. Etsi lausekkeen arvo: log6 4 + log6 9.

Koska logaritmien kantaluvut ovat samat, käytämme summakaavaa:
log6 4 + log6 9 = log6 (4 9) = log6 36 = 2.

Tehtävä. Etsi lausekkeen arvo: log2 48 − log2 3.

Perusteet ovat samat, käytämme erokaavaa:
log2 48 − log2 3 = log2 (48: 3) = log2 16 = 4.

Tehtävä. Etsi lausekkeen arvo: log3 135 − log3 5.

Jälleen, perusteet ovat samat, joten meillä on:
log3 135 − log3 5 = log3 (135: 5) = log3 27 = 3.

Kuten näet, alkuperäiset lausekkeet koostuvat "huonoista" logaritmeista, joita ei käsitellä erikseen. Mutta muunnosten jälkeen tulee melko normaaleja lukuja. Monet testit perustuvat tähän tosiasiaan. Kyllä, kontrolli - samanlaisia ​​ilmaisuja kaikessa vakavuudessa (joskus - käytännössä ilman muutoksia) tarjotaan kokeessa.

Eksponentin poistaminen logaritmista

Monimutkaistaan ​​nyt tehtävää hieman. Entä jos logaritmin kantaosassa tai argumentissa on aste? Sitten tämän asteen eksponentti voidaan ottaa pois logaritmin etumerkistä seuraavien sääntöjen mukaisesti:

On helppo nähdä, että viimeinen sääntö seuraa heidän kahta ensimmäistä. Mutta on parempi muistaa se joka tapauksessa - joissain tapauksissa se vähentää merkittävästi laskelmien määrää.

Tietysti kaikki nämä säännöt ovat järkeviä, jos ODZ-logaritmia noudatetaan: a > 0, a ≠ 1, x > 0. Ja vielä yksi asia: opi soveltamaan kaikkia kaavoja paitsi vasemmalta oikealle, myös päinvastoin, ts. voit syöttää logaritmin etumerkkiä edeltävät luvut itse logaritmiin.

Kuinka ratkaista logaritmit

Tätä vaaditaan useimmiten.

Tehtävä. Etsi lausekkeen arvo: log7 496.

Päästään eroon argumentin asteesta ensimmäisen kaavan mukaan:
log7 496 = 6 log7 49 = 6 2 = 12

Tehtävä. Etsi lausekkeen arvo:

Huomaa, että nimittäjä on logaritmi, jonka kanta ja argumentti ovat tarkat potenssit: 16 = 24; 49 = 72. Meillä on:

Mielestäni viimeinen esimerkki kaipaa selvennystä. Mihin logaritmit ovat kadonneet? Viimeiseen hetkeen asti työskentelemme vain nimittäjällä. He esittivät siellä seisovan logaritmin kannan ja argumentin asteiden muodossa ja ottivat indikaattorit - he saivat "kolmikerroksisen" murto-osan.

Katsotaan nyt pääosaa. Osoittajalla ja nimittäjällä on sama luku: log2 7. Koska log2 7 ≠ 0, voimme pienentää murto-osaa - 2/4 jää nimittäjään. Aritmeettisten sääntöjen mukaan neljä voidaan siirtää osoittajaan, mikä tehtiin. Tuloksena on vastaus: 2.

Siirtyminen uudelle perustalle

Puhuessani logaritmien yhteen- ja vähennyssäännöistä korostin erityisesti, että ne toimivat vain samoilla perusteilla. Entä jos pohjat ovat erilaiset? Entä jos ne eivät ole täsmälleen saman luvun potenssit?

Uuteen tukikohtaan siirtymisen kaavat tulevat apuun. Muotoilemme ne lauseen muodossa:

Olkoon logaritmin logaksi annettu. Sitten mille tahansa luvulle c, jonka c > 0 ja c ≠ 1, yhtälö on tosi:

Erityisesti, jos laitamme c = x, saamme:

Toisesta kaavasta seuraa, että logaritmin kanta ja argumentti voidaan vaihtaa keskenään, mutta tässä tapauksessa koko lauseke "käännetään" ts. logaritmi on nimittäjässä.

Näitä kaavoja löytyy harvoin tavallisista numeerisista lausekkeista. Niiden käyttökelpoisuutta on mahdollista arvioida vain logaritmiset yhtälöitä ja epäyhtälöitä ratkaistaessa.

On kuitenkin tehtäviä, joita ei voida ratkaista ollenkaan muutoin kuin siirtymällä uudelle perustalle. Tarkastellaanpa paria näistä:

Tehtävä. Etsi lausekkeen arvo: log5 16 log2 25.

Huomaa, että molempien logaritmien argumentit ovat tarkat eksponentit. Otetaan indikaattorit pois: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;

Käännetään nyt toinen logaritmi:

Koska tulo ei muutu tekijöiden permutaatiosta, kerroimme rauhallisesti neljä ja kaksi ja sitten selvitimme logaritmit.

Tehtävä. Etsi lausekkeen arvo: log9 100 lg 3.

Ensimmäisen logaritmin kanta ja argumentti ovat tarkat potenssit. Kirjataan se ylös ja päästään eroon indikaattoreista:

Nyt päästään eroon desimaalilogaritmista siirtymällä uuteen kantaan:

Peruslogaritminen identiteetti

Usein ratkaisuprosessissa on esitettävä luku logaritmina tiettyyn kantaan. Tässä tapauksessa kaavat auttavat meitä:

Ensimmäisessä tapauksessa luvusta n tulee argumentin eksponentti. Luku n voi olla mitä tahansa, koska se on vain logaritmin arvo.

Toinen kaava on itse asiassa parafrasoitu määritelmä. Sitä kutsutaan näin:

Todellakin, mitä tapahtuu, jos lukua b korotetaan siinä määrin, että tämän asteen luku b antaa luvun a? Aivan oikein: tämä on sama numero a. Lue tämä kappale huolellisesti uudelleen - monet ihmiset "roikkuvat" siinä.

Kuten uudet perusmuunnoskaavat, logaritminen perusidentiteetti on joskus ainoa mahdollinen ratkaisu.

Tehtävä. Etsi lausekkeen arvo:

Huomaa, että log25 64 = log5 8 - juuri poisti neliön kannasta ja logaritmin argumentin. Ottaen huomioon potenssien kertomisen säännöt samalla kantalla, saamme:

Jos joku ei ole perillä, tämä oli oikea tehtävä yhtenäisestä valtiokokeesta 🙂

Logaritminen yksikkö ja logaritminen nolla

Lopuksi annan kaksi identiteettiä, joita on vaikea kutsua ominaisuuksiksi - pikemminkin nämä ovat seurauksia logaritmin määritelmästä. Heitä löytyy jatkuvasti ongelmista ja yllättäen ne aiheuttavat ongelmia jopa "edenneille" opiskelijoille.

1. logaa = 1 on. Muista kerta kaikkiaan: logaritmi mihin tahansa kantaan a itse tästä kannasta on yhtä suuri kuin yksi.
2. loga 1 = 0 on. Kanta a voi olla mikä tahansa, mutta jos argumentti on yksi, logaritmi on nolla! Koska a0 = 1 on määritelmän suora seuraus.

Siinä kaikki ominaisuudet. Muista harjoitella niiden toteuttamista käytännössä! Lataa huijauslehti oppitunnin alussa, tulosta se ja ratkaise ongelmat.

Logaritmeja, kuten mitä tahansa lukua, voidaan lisätä, vähentää ja muuntaa kaikin mahdollisin tavoin. Mutta koska logaritmit eivät ole aivan tavallisia lukuja, tässä on säännöt, joita kutsutaan perusominaisuudet.

Nämä säännöt on tunnettava - ilman niitä ei voida ratkaista vakavaa logaritmista ongelmaa. Lisäksi niitä on hyvin vähän - kaikki voidaan oppia yhdessä päivässä. Joten aloitetaan.

Logaritmien yhteen- ja vähennyslasku

Tarkastellaan kahta logaritmia, joilla on sama kanta: log a x ja kirjaudu sisään a y. Sitten ne voidaan lisätä ja vähentää, ja:

1. Hirsi a x+loki a y= loki a (x · y);
2. Hirsi a x-loki a y= loki a (x : y).

Joten logaritmien summa on yhtä suuri kuin tuotteen logaritmi, ja ero on osamäärän logaritmi. Huomaa: avainkohta tässä on - samoilla perusteilla. Jos perusteet ovat erilaiset, nämä säännöt eivät toimi!

Nämä kaavat auttavat sinua laskemaan logaritmisen lausekkeen, vaikka sen yksittäisiä osia ei otettaisi huomioon (katso oppitunti "Mikä on logaritmi"). Katso esimerkkejä ja katso:

loki 6 4 + loki 6 9.

Koska logaritmien kantaluvut ovat samat, käytämme summakaavaa:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Tehtävä. Etsi lausekkeen arvo: log 2 48 − log 2 3.

Perusteet ovat samat, käytämme erokaavaa:
log 2 48 - log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Tehtävä. Etsi lausekkeen arvo: log 3 135 − log 3 5.

Jälleen, perusteet ovat samat, joten meillä on:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Kuten näet, alkuperäiset lausekkeet koostuvat "huonoista" logaritmeista, joita ei käsitellä erikseen. Mutta muunnosten jälkeen tulee melko normaaleja lukuja. Monet testit perustuvat tähän tosiasiaan. Kyllä, kontrolli - samanlaisia ​​ilmaisuja kaikessa vakavuudessa (joskus - käytännössä ilman muutoksia) tarjotaan kokeessa.

Eksponentin poistaminen logaritmista

Monimutkaistaan ​​nyt tehtävää hieman. Entä jos logaritmin kantaosassa tai argumentissa on aste? Sitten tämän asteen eksponentti voidaan ottaa pois logaritmin etumerkistä seuraavien sääntöjen mukaisesti:

On helppo nähdä, että viimeinen sääntö seuraa heidän kahta ensimmäistä. Mutta on parempi muistaa se joka tapauksessa - joissain tapauksissa se vähentää merkittävästi laskelmien määrää.

Tietenkin kaikki nämä säännöt ovat järkeviä, jos ODZ-logaritmia noudatetaan: a > 0, a ≠ 1, x> 0. Ja vielä yksi asia: opettele soveltamaan kaikkia kaavoja ei vain vasemmalta oikealle, vaan myös päinvastoin, ts. voit syöttää logaritmin etumerkkiä edeltävät luvut itse logaritmiin. Tätä vaaditaan useimmiten.

Tehtävä. Etsi lausekkeen arvo: log 7 49 6 .

Päästään eroon argumentin asteesta ensimmäisen kaavan mukaan:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Tehtävä. Etsi lausekkeen arvo:

[Kuvan kuvateksti]

Huomaa, että nimittäjä on logaritmi, jonka kanta ja argumentti ovat tarkat potenssit: 16 = 2 4 ; 49 = 72. Meillä on:

[Kuvan kuvateksti]

Mielestäni viimeinen esimerkki kaipaa selvennystä. Mihin logaritmit ovat kadonneet? Viimeiseen hetkeen asti työskentelemme vain nimittäjällä. He esittivät siellä seisovan logaritmin kannan ja argumentin asteiden muodossa ja ottivat indikaattorit - he saivat "kolmikerroksisen" murto-osan.

Katsotaan nyt pääosaa. Osoittajalla ja nimittäjällä on sama luku: log 2 7. Koska log 2 7 ≠ 0, voimme pienentää murto-osaa - 2/4 jää nimittäjään. Aritmeettisten sääntöjen mukaan neljä voidaan siirtää osoittajaan, mikä tehtiin. Tuloksena on vastaus: 2.

Siirtyminen uudelle perustalle

Puhuessani logaritmien yhteen- ja vähennyssäännöistä korostin erityisesti, että ne toimivat vain samoilla perusteilla. Entä jos pohjat ovat erilaiset? Entä jos ne eivät ole täsmälleen saman luvun potenssit?

Uuteen tukikohtaan siirtymisen kaavat tulevat apuun. Muotoilemme ne lauseen muodossa:

Anna logaritmin lokikirjautua a x. Siis mille tahansa numerolle c sellasta c> 0 ja c≠ 1, yhtälö on totta:

[Kuvan kuvateksti]

Varsinkin jos laitamme c = x, saamme:

[Kuvan kuvateksti]

Toisesta kaavasta seuraa, että logaritmin kanta ja argumentti voidaan vaihtaa keskenään, mutta tässä tapauksessa koko lauseke "käännetään" ts. logaritmi on nimittäjässä.

Näitä kaavoja löytyy harvoin tavallisista numeerisista lausekkeista. Niiden käyttökelpoisuutta on mahdollista arvioida vain logaritmiset yhtälöitä ja epäyhtälöitä ratkaistaessa.

On kuitenkin tehtäviä, joita ei voida ratkaista ollenkaan muutoin kuin siirtymällä uudelle perustalle. Tarkastellaanpa paria näistä:

Tehtävä. Etsi lausekkeen arvo: log 5 16 log 2 25.

Huomaa, että molempien logaritmien argumentit ovat tarkat eksponentit. Otetaan indikaattorit pois: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2 log 2 5;

Käännetään nyt toinen logaritmi:

[Kuvan kuvateksti]

Koska tulo ei muutu tekijöiden permutaatiosta, kerroimme rauhallisesti neljä ja kaksi ja sitten selvitimme logaritmit.

Tehtävä. Etsi lausekkeen arvo: log 9 100 lg 3.

Ensimmäisen logaritmin kanta ja argumentti ovat tarkat potenssit. Kirjataan se ylös ja päästään eroon indikaattoreista:

[Kuvan kuvateksti]

Nyt päästään eroon desimaalilogaritmista siirtymällä uuteen kantaan:

[Kuvan kuvateksti]

Peruslogaritminen identiteetti

Usein ratkaisuprosessissa on esitettävä luku logaritmina tiettyyn kantaan. Tässä tapauksessa kaavat auttavat meitä:

Ensimmäisessä tapauksessa numero n tulee väitteen eksponentti. Määrä n voi olla mitä tahansa, koska se on vain logaritmin arvo.

Toinen kaava on itse asiassa parafrasoitu määritelmä. Sitä kutsutaan logaritmiseksi perusidentiteetiksi.

Todellakin, mitä tapahtuu, jos numero b nosta valtaan niin, että b tässä määrin antaa numeron a? Aivan oikein: tämä on sama numero a. Lue tämä kappale huolellisesti uudelleen - monet ihmiset "roikkuvat" siinä.

Kuten uudet perusmuunnoskaavat, logaritminen perusidentiteetti on joskus ainoa mahdollinen ratkaisu.

Tehtävä. Etsi lausekkeen arvo:

[Kuvan kuvateksti]

Huomaa, että log 25 64 = log 5 8 - juuri poisti neliön kannasta ja logaritmin argumentin. Ottaen huomioon potenssien kertomisen säännöt samalla kantalla, saamme:

[Kuvan kuvateksti]

Jos joku ei ole perillä, tämä oli todellinen tehtävä kokeesta :)

Logaritminen yksikkö ja logaritminen nolla

Lopuksi annan kaksi identiteettiä, joita on vaikea kutsua ominaisuuksiksi - pikemminkin nämä ovat seurauksia logaritmin määritelmästä. Heitä löytyy jatkuvasti ongelmista ja yllättäen ne aiheuttavat ongelmia jopa "edenneille" opiskelijoille.

1. Hirsi a a= 1 on logaritminen yksikkö. Muista kerta kaikkiaan: logaritmi mihin tahansa kantaan a tästä perustasta itse on yhtä suuri kuin yksi.
2. Hirsi a 1 = 0 on logaritminen nolla. Pohja a voi olla mikä tahansa, mutta jos argumentti on yksi, logaritmi on nolla! koska a 0 = 1 on suora seuraus määritelmästä.

Siinä kaikki ominaisuudet. Muista harjoitella niiden toteuttamista käytännössä! Lataa huijauslehti oppitunnin alussa, tulosta se ja ratkaise ongelmat.

Positiivisen luvun b logaritmi kantaan a (a>0, a ei ole yhtä suuri kuin 1) on luku c siten, että ac = b: log ab = c ⇔ ac = b (a > 0, a ≠ 1, b > 0)       

Huomaa, että ei-positiivisen luvun logaritmia ei ole määritelty. Lisäksi logaritmin kantaluvun on oltava positiivinen luku, joka ei ole yhtä suuri kuin 1. Jos esimerkiksi neliöimme -2, saamme luvun 4, mutta tämä ei tarkoita, että 4:n kanta -2 logaritmi olisi 2.

Peruslogaritminen identiteetti

a log a b = b (a > 0, a ≠ 1) (2)

On tärkeää, että tämän kaavan oikean ja vasemman osan määritelmäalueet ovat erilaiset. Vasen puoli on määritelty vain b>0:lle, a>0:lle ja a ≠ 1:lle. Oikea puoli on määritelty mille tahansa b:lle, eikä se riipu a:sta ollenkaan. Siten peruslogaritmisen "identiteetin" käyttäminen yhtälöiden ja epäyhtälöiden ratkaisemisessa voi johtaa DPV:n muutokseen.

Kaksi ilmeistä logaritmin määritelmän seurausta

log a a = 1 (a > 0, a ≠ 1) (3)
log a 1 = 0 (a > 0, a ≠ 1) (4)

Todellakin, kun nostetaan lukua a ensimmäiseen potenssiin, saamme saman luvun, ja kun nostetaan se nollapotenssiin, saamme yhden.

Tulon logaritmi ja osamäärän logaritmi

log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0) (5)

Log a b c = log a b − log a c (a > 0, a ≠ 1, b > 0, c > 0) (6)

Haluaisin varoittaa koululaisia ​​näiden kaavojen ajattelemattomasta käytöstä logaritmisen yhtälöiden ja epäyhtälöiden ratkaisemisessa. Kun niitä käytetään "vasemmalta oikealle", ODZ kapenee, ja kun siirrytään logaritmien summasta tai erosta tulon tai osamäärän logaritmiin, ODZ laajenee.

Itse asiassa lauseke log a (f (x) g (x)) määritellään kahdessa tapauksessa: kun molemmat funktiot ovat ehdottomasti positiivisia tai kun f(x) ja g(x) ovat molemmat pienempiä kuin nolla.

Muuntamalla tämä lauseke summaksi log a f (x) + log a g (x) , joudumme rajoittumaan vain tapaukseen, jossa f(x)>0 ja g(x)>0. Hyväksyttyjen arvojen vaihteluväli on kaventunut, eikä tätä voida kategorisesti hyväksyä, koska se voi johtaa ratkaisujen menettämiseen. Samanlainen ongelma on kaavalla (6).

Aste voidaan ottaa pois logaritmin etumerkistä

log a b p = p log a b (a > 0, a ≠ 1, b > 0) (7)

Ja taas haluaisin vaatia tarkkuutta. Harkitse seuraavaa esimerkkiä:

Log a (f (x) 2 = 2 log a f (x)

Yhtälön vasen puoli on luonnollisesti määritelty kaikille f(x):n arvoille nollaa lukuun ottamatta. Oikea puoli on vain f(x)>0! Ottamalla teho pois logaritmista, kavennetaan jälleen ODZ:tä. Käänteinen menettely johtaa sallittujen arvojen alueen laajentamiseen. Kaikki nämä huomautukset eivät koske vain 2:n potenssia, vaan myös mitä tahansa parillista potenssia.

Kaava muuttaa uuteen tukikohtaan

log a b = log c b log c a (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1) (8)

Se harvinainen tapaus, jolloin ODZ ei muutu muuntamisen aikana. Jos olet valinnut kannan c viisaasti (positiivinen eikä yhtä suuri kuin 1), kaava uuteen kantaan siirtymiseen on täysin turvallinen.

Jos valitsemme luvun b uudeksi kantaksi c, saamme tärkeän kaavan (8) erikoistapauksen:

Log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1) (9)

Muutamia yksinkertaisia ​​esimerkkejä logaritmeilla

Esimerkki 1 Laske: lg2 + lg50.
Ratkaisu. lg2 + lg50 = lg100 = 2. Käytimme logaritmien summan kaavaa (5) ja desimaalilogaritmin määritelmää.

Esimerkki 2 Laske: lg125/lg5.
Ratkaisu. lg125/lg5 = log 5 125 = 3. Käytimme uutta kantasiirtymäkaavaa (8).

Taulukko logaritmiin liittyvistä kaavoista

a log a b = b (a > 0, a ≠ 1)

log a a = 1 (a > 0, a ≠ 1)

log a 1 = 0 (a > 0, a ≠ 1)

log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0)

log a b c = log a b − log a c (a > 0, a ≠ 1, b > 0, c > 0)

log a b p = p log a b (a > 0, a ≠ 1, b > 0)

log a b = log c b log c a (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1)

log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1)

*Maisteriopiskelija Isakhova A.A.:n tieteellisessä valvonnassa,PhD matemaattinen ja tietokonemallinnus

Oletko koskaan ajatellut, kuinka ihmiset laskivat muinaisina aikoina, jolloin ei ollut laskimia tai tietokoneita? Laskelmat tehtiin manuaalisesti, paperilla tai henkisesti. Vaikka heidän kohtaamat haasteet olivat yhtä monimutkaisia ​​kuin nykyään.

Tietokoneiden puute pakotti muinaiset matemaatikot yksinkertaistamaan laskelmia. He keksivät taulukoita, joissa oli jo laskettuja lausekkeita (esimerkiksi kertotaulukko), etsivät tapoja korvata monimutkaiset toiminnot yksinkertaisilla. Tänään puhumme yhdestä sellaisesta "yksinkertaistamisesta" tai siitä, kuinka ihmiset ovat oppineet korvaamaan kertolaskua yhteenlaskemalla ja jakamista vähentämällä. Tämän seurauksena logaritmi keksittiin. Ymmärtääksesi, mikä se on, sinun on otettava vain kolme vaihetta.

VAIHE 1: Yksinkertaista ja yksinkertaista uudelleen

Aloitetaan yksinkertaisella esimerkillä.

2 + 2 = 4

Monimutkaistaan ​​ongelmaa ja etsitään viiden kaksin summa.

2 + 2 + 2 + 2 + 2 = 10

Ja selvisimme tästä tehtävästä helposti. Ja jos sinun on löydettävä 1 000 000 kaksikon summa? Samankaltaisen laskentamenetelmän käyttäminen vie paljon tilaa ja aikaa. Mutta ovelat matemaatikot ovat ymmärtäneet, kuinka helppoa se on tehdä. He keksivät kertolaskuoperaation. Katsotaan miltä se näyttää:

2 × 2 × 2 × 2 × 2 × 2 × 2 = 128

Tämän lausekkeen yksinkertaistamiseksi matemaatikot keksivät eksponentiotoiminnon. On selvää, että puhumme saman luvun kertomisesta itsestään n kertaa, miksi monistaa se ja kirjoittaa se uudelleen ja uudelleen? Eikö näin ole helpompi kirjoittaa?

Tässä a- tutkinnon perusta n- eksponentti. Näin ollen olemme lyhentäneet ennätystä merkittävästi. Eksponentin arvosta riippumatta lauseke näyttää erittäin ytimekkäältä:

Michael Stiefel(1487-1567) - Saksalainen matemaatikko, antoi merkittävän panoksen algebran ja sen alueiden, kuten progression, eksponentioinnin ja negatiivisten lukujen, kehitykseen. Stiefel käytti ensimmäisenä käsitteitä "eksponentti" ja "juuri". Huolimatta siitä, että tiedemies todella käytti logaritmeja, löytäjän maine meni skotlantilaiselle matemaatikolle John Napierille (1550–1617).

VAIHE 2: Ymmärrä valtuuksien ominaisuudet

Kuten olemme jo todenneet, muinaiset matemaatikot eivät kuormittaneet itseään laskelmilla joka kerta, kun heidän piti kertoa tai lisätä numeroita, vaan käyttivät taulukoita ennalta lasketuilla tuloksilla. Erittäin mukavasti! Käyttämällä samanlaista taulukkoa saksalainen matemaatikko Michael Stiefel huomasi mielenkiintoisen kuvion aritmeettisen ja geometrisen progression välillä.

Aritmeettinen progressio	1	2	3	4	5	6	7	8	9	10
Geometrinen eteneminen	2	4	8	16	32	64	128	256	512	1024
Tehon merkintä	2 1	2 2	2 3	2 4	2 5	2 6	2 7	2 8	2 9	2 10

Kokeillaan ja katsotaan. Loppujen lopuksi tämä säännöllisyys mahdollistaa toimintojen yksinkertaistamisen kertominen ja jako. Oletetaan, että meidän on laskettava kahden luvun tulo:

16 × 64 =  ?

Ennen kuin teet mitään laskelmia, katso taulukkoa ja löydä nämä luvut: nämä ovat geometrisen progression jäseniä, joiden askel on 2. Numerot niiden yläpuolella ylärivillä: 4 yli 16; 6 yli 64 on jäseniä aritmeettinen progressio. Lisätään nämä luvut: 4 + 6 = 10. Nyt katsotaan mikä luku on luvun 10 alla toisella rivillä - 1024. Mutta jos suoritamme aloitustehtävämme 16x64, niin tuloksena on 1024. Tämä tarkoittaa, että käyttämällä taulukosta ja koska pystyt vain laskemaan yhteen numerot, löydät tuotteen helposti.

Mieti nyt jakotoimintoa:

Katso taulukkoa uudelleen ja etsi vastaavat numerot yläriviltä. Saamme 10 ja 7 vastaavasti. Jos lisäämme kertomalla, niin jakamalla vähennämme: 10–7  =  3. Katsomme toisella rivillä luvun 3 alla olevaa lukua, tämä on 8. Siksi 1024:128 = 8.

Vastaavasti voit käyttää taulukkoa operaatioihin eksponentio ja juurien erottaminen.

Esimerkiksi meidän on tehtävä neliö 32. Katsomme ylärivillä olevaa numeroa 32:n yläpuolella. Saamme 5. Kerromme 5:llä 2. Osoittautuu 10, sitten katsotaan 10:n alapuolella olevaa lukua: 1024. Näin ollen 32 2   = 1024.

Harkitse juuren purkamista. Etsitään esimerkiksi luvun 512 kolmannen asteen juuri. Ylärivillä olevan luvun 512 yläpuolella on 9. Jaa 9 kolmella, saadaan 3. Etsi vastaava luku toiselta riviltä. Saamme 8. Siksi 83 = 512.

Kaikki neljä esimerkkiä ovat seurausta asteiden ominaisuuksista, jotka voidaan kirjoittaa seuraavasti:

VAIHE 3: Kutsutaan sitä logaritmiksi

Kun valtuuksia on käsitelty, yritetään ratkaista pieni yhtälö:

2 x = 4

Tätä yhtälöä kutsutaan paljastava. Koska X, joka meidän on löydettävä indikaattori potenssi, johon 2 on nostettava, jotta saadaan 4. Yhtälön x  = 2 ratkaisu.

Harkitse toista samanlaista esimerkkiä:

2x = 5

Sanotaanpa ehto uudelleen, etsimme lukua x, johon 2 on nostettava, jotta saadaan 5. Tämä kysymys saa meidät tyrmistymään. Ratkaisu on varmasti olemassa, jos esimerkiksi piirrät kaavioita näistä funktioista, niin ne leikkaavat. Mutta löytääksemme sen, meidän on etsittävä sitä yrityksen ja erehdyksen avulla. Ja se voi kestää kauan.

Siksi muinaiset tiedemiehet keksivät logaritmin, he tiesivät, että yhtälön ratkaisu on olemassa, mutta sitä ei aina tarvittu heti. Matemaattisesti tämä on kirjoitettu näin: x  =  log 2 5. Löysimme siis yhtälön ratkaisun 2 x   = 5. Vastaus: x  =  log 2 5. Jos annat tarkan vastauksen, niin x = 2.32192809489…, eikä tämä murto-osa lopu koskaan.

Ilmaus kuuluu näin: kanta 2 logaritmi 5:stä. Tämän muistaminen on helppoa: kanta kirjoitetaan aina alareunaan, sekä eksponentiaalisilla että logaritmisilla merkinnöillä.

Logaritmin ominaisuudet

Logaritmeilla on rajoituksia. Matematiikassa on kaksi kovaa rajaa.

a) Et voi jakaa nollalla

b) Ota negatiivisen luvun parillinen juuri(koska negatiivinen luku neliö on aina positiivinen).

on sama kuin kirjoittaminen

a x = b

Rajoitukset a

a on kanta, joka nostetaan x potenssiin, jotta saadaan b.

Jos a  = 1,1 mihin tahansa potenssiin antaa yhden.

Entä jos a on pienempi kuin nolla? Negatiiviset luvut ovat oikeita. Niitä voidaan nostaa yhteen asteeseen, ei toiseen. Siksi jätämme ne myös pois. Tuloksena saadaan: a > 0; a ≠ 1

Rajoitukset b

Jos positiivinen luku korotetaan mihin tahansa potenssiin, saadaan myös positiivinen luku. Näin ollen: b  > 0. x voi olla mikä tahansa luku, koska voimme nostaa mihin tahansa potenssiin.

Jos b  = 1, niin x = 0 mille tahansa a:lle.

Toiminnot logaritmille

Ottaen huomioon potenssien perusominaisuudet, johdetaan logaritmeille vastaavat:

Summa. Tuloksen logaritmi on yhtä suuri kuin tekijöiden logaritmien summa:

Ero. Osamäärän logaritmi on yhtä suuri kuin osingon ja jakajan logaritmien välinen ero:

Tutkinto. Potentin logaritmi on yhtä suuri kuin eksponentin ja sen kantaluvun logaritmi.