Fluktuacije u broju grabežljivaca i plijena. Oscilacije sistema grabežljivac-plijen (Lotka-Voltaire model). Simulacijsko modeliranje sistema "Predator-Prey".
Dom Predation - oblik trofičkih odnosa između organizama različite vrste , za koje je jedan od njih ( predator ) napada drugog (žrtva
) i hrani se svojim mesom, odnosno obično se radi o činu ubijanja žrtve. Sistem predator-plijen
- složen ekosistem za koji se ostvaruju dugoročni odnosi između vrsta grabežljivaca i plijena, tipičan primjer koevolucije. Koevolucija - zajednička evolucija biološke vrste
, u interakciji u ekosistemu.
Odnos između grabežljivaca i njihovog plijena razvija se ciklično, ilustrirajući neutralnu ravnotežu.
1. Jedini ograničavajući faktor koji ograničava reprodukciju plijena je pritisak grabežljivaca na njih. Ne uzimaju se u obzir ograničeni resursi okruženja za žrtvu.
2. Razmnožavanje grabežljivaca je ograničeno količinom hrane koju dobijaju (broj žrtava).
U svojoj srži, Lotka-Volterra model je matematički opis darvinističkog principa borbe za postojanje. Volterra-Lotka sistem, koji se često naziva sistem grabežljivac-plijen, opisuje interakciju dvije populacije - grabežljivaca (na primjer, lisice) i plijena (na primjer, zečevi), koji žive prema malo drugačijim "zakonima". Plijen održava svoju populaciju jelom prirodni resurs
, kao što su trave, što dovodi do eksponencijalnog rasta populacije ako nema predatora. Predatori održavaju svoju populaciju samo “jedući” svoje žrtve. Stoga, ako populacija plijena nestane, tada se populacija predatora eksponencijalno smanjuje. Jedenje plijena od strane grabežljivaca oštećuje populaciju plijena, ali u isto vrijeme pruža dodatni resurs za reprodukciju grabežljivaca.
Pitanje
PRINCIP MINIMALNE VELIČINE STANOVNIŠTVA
pojava koja prirodno postoji u prirodi, karakterizirana kao jedinstveni prirodni princip, što znači da svaka životinjska vrsta ima specifičnu minimalnu veličinu populacije, čije kršenje ugrožava postojanje populacije, a ponekad i vrste u cjelini. leži u činjenici da se populacija ne može neograničeno povećavati, zbog iscrpljivanja resursa hrane i uslova reprodukcije (Andrevarta-Birch teorija) i ograničenja uticaja kompleksa abiotskih i biotičkih faktora sredine (Fredericksova teorija).
, kao što su trave, što dovodi do eksponencijalnog rasta populacije ako nema predatora. Predatori održavaju svoju populaciju samo “jedući” svoje žrtve. Stoga, ako populacija plijena nestane, tada se populacija predatora eksponencijalno smanjuje. Jedenje plijena od strane grabežljivaca oštećuje populaciju plijena, ali u isto vrijeme pruža dodatni resurs za reprodukciju grabežljivaca.
Dakle, kao što je već bilo jasno Fibonačiju, rast populacije je proporcionalan njegovoj veličini, pa prema tome, ako rast populacije nije ograničen ničim vanjski faktori, neprekidno ubrzava. Hajde da opišemo ovaj rast matematički.
Rast populacije je proporcionalan broju jedinki u njemu, odnosno Δ N~N, Gdje N- veličina populacije i Δ N- njegova promjena u određenom vremenskom periodu. Ako je ovaj period beskonačno mali, možemo to napisati dN/dt=r × N , Gdje dN/dt- promjena veličine populacije (rast), i r - reproduktivni potencijal, varijabla koja karakterizira sposobnost populacije da poveća svoju veličinu. Zadata jednačina se zove eksponencijalni model rast stanovništva (slika 4.4.1).
Sl.4.4.1. Eksponencijalni rast.
Kao što je lako razumjeti, kako vrijeme raste, populacija raste sve brže, a ubrzo juri u beskonačnost. Naravno, nijedno stanište ne može podržati postojanje populacije sa beskonačnim brojem. Međutim, postoji niz procesa rasta populacije koji se, u određenom vremenskom periodu, mogu opisati eksponencijalnim modelom. Govorimo o slučajevima neograničenog rasta, kada neka populacija naseljava okolinu s viškom slobodnih resursa: krave i konji naseljavaju pampu, brašnaste bube naseljavaju elevator za žito, kvasac naseljavaju bocu soka od grožđa itd.
Naravno, eksponencijalni rast stanovništva ne može trajati vječno. Prije ili kasnije resursi će biti iscrpljeni, a rast stanovništva će se usporiti. Kakvo će biti ovo kočenje? Praktična ekologija poznaje razne mogućnosti: nagli porast brojnosti praćen izumiranjem populacije koja je iscrpila svoje resurse i postepeno usporavanje rasta kako se približava određenom nivou. Najlakši način da se to opiše je sporo kočenje. Najjednostavniji model koji opisuje takvu dinamiku se zove logistika a predložio ga je (da opiše rast ljudske populacije) francuski matematičar Verhulst davne 1845. Godine 1925., sličan obrazac je ponovo otkrio američki ekolog R. Pearl, koji je sugerirao da je univerzalan.
U logistički model se uvodi varijabla K- srednji kapacitet, ravnotežna veličina populacije pri kojoj ona troši sve raspoložive resurse. Povećanje logističkog modela opisano je jednadžbom dN/dt=r × N × (K-N)/K (Slika 4.4.2).

Rice. 4.4.2. Rast logistike
ćao N je mali, na rast stanovništva uglavnom utiče faktor r× N a rast stanovništva se ubrzava. Kada postane dovoljno visoka, faktor počinje uglavnom da utiče na veličinu populacije (K-N)/K i rast stanovništva počinje da se usporava. Kada N=K, (K-N)/K=0 i rast stanovništva prestaje.
Uz svu svoju jednostavnost, logistička jednadžba na zadovoljavajući način opisuje mnoge slučajeve uočene u prirodi i još uvijek se uspješno koristi u matematičkoj ekologiji.
Br. 16. Strategija ekološkog preživljavanja- evolucijski razvijen skup svojstava populacije čiji je cilj povećanje vjerovatnoće preživljavanja i ostavljanja potomstva.
Dakle, A.G. Ramensky (1938) razlikuje tri glavna tipa strategija preživljavanja među biljkama: nasilne, pacijente i eksplerente.
Nasilnici (siloviki) - potiskuju sve konkurente, na primjer, drveće koje formira autohtone šume.
Bolesnici su vrste koje mogu preživjeti u nepovoljnim uvjetima („sjenoljubivi”, „sololjubivi” itd.).
Eksplerenti (punila) su vrste koje se brzo mogu pojaviti tamo gdje su autohtone zajednice poremećene - na čistinama i opožarenim područjima (jasika), na plićaku itd.
Strategije zaštite životne sredine populacije se razlikuju velika raznolikost. Ali u isto vrijeme, sva njihova raznolikost leži između dva tipa evolucijske selekcije, koja se označavaju konstantama logističke jednadžbe: r-strategije i K-strategije.
| Potpiši | r-strategije | K-strategije |
| Mortalitet | Ne zavisi od gustine | Zavisi od gustine |
| Konkurencija | Slabo | Akutna |
| Životni vijek | Kratko | Dugo |
| Brzina razvoja | Brzo | Sporo |
| Vrijeme reprodukcije | Rano | Kasno |
| Reproduktivno poboljšanje | Slabo | Veliki |
| Tip krivulje preživljavanja | Konkavna | Konveksna |
| Veličina tijela | Mala | Veliki |
| Karakter potomstva | Mnogo, malo | Mali, veliki |
| Veličina populacije | Jake fluktuacije | Konstantno |
| Preferirano okruženje | Promjenjivo | Konstantno |
| Faze sukcesije | Rano | Kasno |
Povezane informacije.
Modeli interakcije dva tipa
Volterrine hipoteze. Analogije s kemijskom kinetikom. Volterra modeli interakcija. Klasifikacija tipova interakcija Konkurencija. Predator-plijen. Generalizirani modeli interakcija vrsta . Kolmogorov model. MacArthurov model interakcije između dvije vrste insekata. Parametrijski i fazni portreti Bazykinovog sistema.
Osnivač moderne matematičke teorije populacija s pravom se smatra italijanski matematičar Vito Volterra, koji je razvio matematičku teoriju bioloških zajednica, čiji su aparat diferencijalne i integro-diferencijalne jednadžbe.(Vito Volterra. Lecons sur la Theorie Mathematique de la Lutte pour la Vie. Pariz)., 1931). U narednim decenijama, dinamika stanovništva razvijala se uglavnom u skladu sa idejama izraženim u ovoj knjizi. Ruski prijevod Volterrine knjige objavljen je 1976. pod naslovom: „ Matematička teorija borba za egzistenciju” sa pogovorom Yu.M. Svirezhev, koji ispituje istoriju razvoja matematičke ekologije u periodu 1931–1976.
Volterrina knjiga je napisana onako kako su napisane knjige o matematici. Prvo formuliše neke pretpostavke o matematičkim objektima koji bi trebalo da se proučavaju, a zatim sprovodi matematičku studiju svojstava ovih objekata.
Sistemi koje je Volterra proučavao sastoje se od dva ili više tipova. U nekim slučajevima se uzima u obzir nabavka upotrebljene hrane. Jednačine koje opisuju interakciju ovih tipova zasnivaju se na sljedećim konceptima.
Volterrine hipoteze
1. Hrana je ili dostupna u neograničenim količinama, ili je njena nabavka striktno regulisana tokom vremena.
2. Jedinke svake vrste odumiru na način da konstantan udio postojećih jedinki umire u jedinici vremena.
3. Predatorske vrste jedu žrtve, a po jedinici vremena broj pojedenih žrtava je uvijek proporcionalan vjerovatnoći susreta jedinki ove dvije vrste, tj. proizvod broja grabežljivaca i broja plijena.
4. Ako postoji hrana u ograničenim količinama i nekoliko vrsta koje su u mogućnosti da je konzumiraju, tada je udio hrane koju pojedini vrsta konzumira u jedinici vremena proporcionalan broju jedinki ove vrste, uzeto sa određenim koeficijentom u zavisnosti od vrste (modeli međuvrsne konkurencije).
5. Ako se vrsta hrani hranom dostupnom u neograničenim količinama, povećanje broja vrsta u jedinici vremena je proporcionalno broju vrste.
6. Ako se vrsta hrani hranom dostupnom u ograničenim količinama, tada se njena reprodukcija reguliše brzinom konzumiranja hrane, tj. po jedinici vremena, povećanje je proporcionalno količini pojedene hrane.
Analogije s kemijskom kinetikom
Ove hipoteze imaju bliske paralele sa hemijskom kinetikom. U jednadžbama dinamike populacije, kao i u jednadžbama kemijske kinetike, koristi se „princip sudara“, kada je brzina reakcije proporcionalna proizvodu koncentracija reagujućih komponenti.
Zaista, prema Volterrinim hipotezama, brzina proces Istrebljenje svake vrste proporcionalno je broju vrsta. U hemijskoj kinetici to odgovara monomolekulskoj reakciji raspadanja određene supstance, au matematičkom modelu odgovara negativnim linearnim članovima na desnim stranama jednadžbi.
Prema konceptima hemijske kinetike, brzina bimolekularne reakcije interakcije između dve supstance proporcionalna je verovatnoći sudara ovih supstanci, tj. proizvod njihove koncentracije. Na isti način, u skladu s Volterrinim hipotezama, stopa reprodukcije grabežljivaca (smrt plijena) proporcionalna je vjerovatnoći susreta grabežljivaca i jedinki plijena, tj. proizvod njihovog broja. U oba slučaja, bilinearni članovi se pojavljuju u modelskom sistemu na desnoj strani odgovarajućih jednačina.
Konačno, linearni pozitivni članovi na desnoj strani Volterrine jednačine, koji odgovaraju rastu populacije pod neograničenim uslovima, odgovaraju autokatalitičkim članovima hemijske reakcije. Ova sličnost jednačina u hemijskim modelima i modelima životne sredine omogućava nam da primenimo iste istraživačke metode za matematičko modeliranje kinetike populacije kao i za sisteme hemijskih reakcija.
Klasifikacija tipova interakcija
U skladu s Volterrinim hipotezama, interakcija dvije vrste, čiji je broj x 1 i x 2 se može opisati jednadžbama:
(9.1)
Evo parametara a i - konstante vlastite stope rasta vrste, c i‑ konstante samoograničavanja brojeva (intraspecifična konkurencija), b ij- konstante interakcije vrsta, (i, j= 1,2). Znaci ovih koeficijenata određuju vrstu interakcije.
U biološkoj literaturi, interakcije se obično klasifikuju prema uključenim mehanizmima. Raznolikost je ovdje ogromna: razne trofičke interakcije, kemijske interakcije koje postoje između bakterija i planktonskih algi, interakcije gljiva s drugim organizmima, sukcesija biljnih organizama, posebno povezana s nadmetanjem za sunčeva svetlost i sa evolucijom tla, itd. Ova klasifikacija izgleda opsežna.
E . Odum je, uzimajući u obzir modele koje je predložio V. Volterra, predložio klasifikaciju ne po mehanizmima, već prema rezultatima. Prema ovoj klasifikaciji, odnose treba ocijeniti kao pozitivne, negativne ili neutralne u zavisnosti od toga da li se brojnost jedne vrste povećava, smanjuje ili ostaje nepromijenjena u prisustvu druge vrste. Tada se glavne vrste interakcija mogu predstaviti u obliku tabele.
VRSTE INTERAKCIJE VRSTA
|
SIMBIOZA |
b 12 ,b 21 >0 |
||
|
KOMENZALIZAM |
b 12 ,>0, b 21 =0 |
||
|
PREDATOR-ŽRTVA |
b 12 ,>0, b 21 <0 |
||
|
AMENSALIZAM |
b 12 ,=0, b 21 <0 |
||
|
KONKURENCIJA |
b 12 , b 21 <0 |
||
|
NEUTRALIZAM |
b 12 , b 21 =0 |
Posljednja kolona pokazuje znakove koeficijenata interakcije iz sistema (9.1)
Pogledajmo glavne vrste interakcija
JEDNAČINE TAKMIČENJA:
Kao što smo videli u 6. predavanju, jednačine takmičenja su:
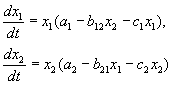 (9.2)
(9.2)
Stacionarna sistemska rješenja:
(1).
![]()
Izvor koordinata, za bilo koje sistemske parametre, je nestabilan čvor.
(2).
![]() (9.3)
(9.3)
C stacionarno stanje (9.3) je sedlo na a 1 >b 12 /Sa 2 i
stabilan čvor na a 1 12 /s 2 . Ovo stanje znači da vrsta izumire ako je njena stopa rasta manja od određene kritične vrijednosti.
(3).
![]() (9.4)
(9.4)
C stacionarno rješenje (9.4)¾ sedlo na a 2 >b 21 /c 1 i stabilan čvor na a 2< b 21 /c 1
(4).
![]() (9.5)
(9.5)
Stacionarno stanje (9.5) karakterizira koegzistenciju dvije konkurentske vrste i predstavlja stabilan čvor ako je relacija zadovoljena:
![]()
Ovo implicira nejednakost:
b 12
b 21
omogućavajući nam da formulišemo uslov koegzistencije vrsta:
Proizvod koeficijenata međupopulacijske interakcije manji je od proizvoda koeficijenata unutar populacijske interakcije.
Zaista, neka se razmatraju prirodne stope rasta dvije vrstea 1 ,a 2 su isti. Tada će biti neophodan uslov za stabilnost
c 2 > b 12 ,c 1 >b 21 .
Ove nejednakosti pokazuju da povećanje veličine jednog konkurenta više potiskuje vlastiti rast nego rast drugog konkurenta. Ako je broj obje vrste ograničen, djelomično ili potpuno, različitim resursima, gore navedene nejednakosti vrijede. Ako obje vrste imaju potpuno iste potrebe, onda će jedna od njih biti održivija i istisnut će svog konkurenta.
Ponašanje faznih putanja sistema daje jasnu predstavu o mogućim ishodima takmičenja. Izjednačimo desnu stranu jednadžbe sistema (9.2) sa nulom:
x 1 (a 1 –c 1 x 1 – b 12 x 2) = 0 (dx 1 /dt = 0),
x 2 (a 2 –b 21 x 1 – c 2 x 2) = 0 (dx 2 /dt = 0),
U ovom slučaju dobijamo jednačine za glavne izokline sistema
x 2 = – b 21 x 1 / c 2 +a 2 /c 2, x 2 = 0
– jednadžbe izoklina vertikalnih tangenta.
x 2 = – c 1 x 1 / b 12 + a 1 /b 12 , x 1 = 0
– jednadžbe izoklina vertikalnih tangenta. Tačke parnog preseka izoklina vertikalnih i horizontalnih tangentnih sistema predstavljaju stacionarna rešenja sistema jednačina (9.2.), a njihove koordinate ![]() su stacionarni brojevi konkurentskih vrsta.
su stacionarni brojevi konkurentskih vrsta.
Moguća lokacija glavnih izoklina u sistemu (9.2) prikazana je na slici 9.1. Rice. 9.1Aodgovara opstanku vrstex 1, sl. 9.1 b– opstanak vrstex 2, sl. 9.1 V– koegzistencija vrsta kada je uslov (9.6) zadovoljen. Slika 9.1Gdemonstrira sistem okidača. Ovdje ishod takmičenja zavisi od početnih uslova. Stacionarno stanje različito od nule (9.5) za oba tipa je nestabilno. Ovo je sedlo kroz koje prolazi separatrica, odvajajući područja preživljavanja svake vrste.

Rice. 9.1.Položaj glavnih izoklina na faznom portretu Volterra sistema konkurencije dva tipa (9.2) sa različitim omjerima parametara. Objašnjenja u tekstu.
Kako bi se proučavala konkurencija vrsta, eksperimenti su provedeni na velikom broju organizama. Obično se biraju dvije blisko srodne vrste i uzgajaju zajedno i odvojeno pod strogo kontroliranim uvjetima. U određenim intervalima vrši se potpuni ili selektivni popis stanovništva. Podaci iz nekoliko ponovljenih eksperimenata se snimaju i analiziraju. Istraživanja su provedena na protozoama (posebno cilijatima), mnogim vrstama buba iz roda Tribolium, drozofila i slatkovodnih rakova (dafnije). Provedeni su mnogi eksperimenti na mikrobnim populacijama (vidi predavanje 11). Eksperimenti su takođe izvedeni u prirodi, uključujući planarijance (Reynolds), dvije vrste mrava (Pontin) itd. Na sl. 9.2. prikazuje krivulje rasta dijatomeja koji koriste isti resurs (koji zauzimaju istu ekološku nišu). Kada se uzgaja u monokulturi Asterionella Formosa dostiže konstantan nivo gustine i održava koncentraciju resursa (silikata) na konstantno niskom nivou. B. Kada se uzgaja u monokulturi Synedrauina ponaša se na sličan način i održava koncentraciju silikata na još nižoj razini. B. Tokom kokultivacije (u duplikatu) Synedrauina istiskuje Asterionella formosa. Očigledno Synedra

Rice. 9.2.Takmičenje u dijatomejima. A - kada se uzgaja u monokulturi Asterionella Formosa dostiže konstantan nivo gustine i održava koncentraciju resursa (silikata) na konstantno niskom nivou. b ‑ kada se uzgaja u monokulturi Synedrauina ponaša se na sličan način i održava koncentraciju silikata na još nižoj razini. V - sa kokultivacijom (u duplikatu) Synedruina istiskuje Asterionella formosa. Očigledno Synedra pobjeđuje u konkurenciji zbog svoje sposobnosti da potpunije iskoristi supstrat (vidjeti također predavanje 11).
Eksperimenti G. Gausea o proučavanju konkurencije su nadaleko poznati, pokazujući opstanak jedne od konkurentskih vrsta i omogućavajući mu da formuliše „zakon kompetitivne isključenosti“. Zakon kaže da samo jedna vrsta može postojati u jednoj ekološkoj niši. Na sl. 9.3. Rezultati Gauseovih eksperimenata su prikazani za dvije vrste Parametiuma, koje zauzimaju istu ekološku nišu (sl. 9.3 a, b) i vrste koje zauzimaju različite ekološke niše (slika 9.3 c).

Rice. 9.3. A- Krivulje rasta populacije dvije vrste Parametium u jednovrstnim usjevima. Crni krugovi - P Aurelija, bijeli krugovi – P. Caudatum
b- Krivulje rasta P Aurelije i P . Caudatum u mešovitoj kulturi.
Gause, 1934
Model konkurencije (9.2) ima nedostatke, a posebno proizilazi da je koegzistencija dvije vrste moguća samo ako je njihov broj ograničen različitim faktorima, ali model ne pokazuje koliko velike razlike moraju biti da bi se osigurala dugoročna koegzistencija. . Istovremeno, poznato je da je za dugotrajan suživot u promjenjivom okruženju neophodna razlika koja dostiže određenu veličinu. Uvođenje stohastičkih elemenata u model (na primjer, uvođenje funkcije korištenja resursa) omogućava nam da kvantitativno istražimo ova pitanja.
Sistem PREDATOR+ŽRTVA
 (9.7)
(9.7)
Ovdje su, za razliku od (9.2), predznaci b 12 I b 21 se razlikuje. Kao iu slučaju konkurencije, porijeklo
![]() (9.8)
(9.8)
je posebna tačka tipa nestabilnog čvora. Još tri moguća stabilna stanja:
![]() ,(9.9)
,(9.9)
![]() (9.10)
(9.10)
![]() (9.11)
(9.11)
Dakle, moguće je da preživi samo plijen (9.10), samo grabežljivac (9.9) (ako ima druge izvore hrane) i koegzistencija obje vrste (9.11). Posljednju opciju smo već razmatrali u predavanju 5. Mogući tipovi faznih portreta za sistem predator-plijen prikazani su na Sl. 9.4.
Izokline horizontalnih tangenta su prave linije
x 2 = – b 21 X 1 /c 2 + a 1/c 2, X 2 = 0,
i izokline vertikalnih tangenti– ravno
x 2 = – c 1 X 1 /b 12 + a 2 /b 12 , X 1 = 0.
Stacionarne tačke leže na preseku vertikalnih i horizontalnih tangentnih izoklina.

Od sl. 9.4 (9.7) vidljivo je sljedeće. Sistem predator-plijen može imati stabilan ravnotežni položaj, u kojem o ) Rumska populacija žrtava potpuno je izumrla ( 2 na sl. 9.4 X A). Očigledno, ovakva situacija se može ostvariti samo ako, pored vrste žrtava, X 1 grabežljivac 2 – ima dodatne izvore napajanja. Ova činjenica se u modelu odražava pozitivnim članom na desnoj strani jednačine za x2. Posebne tačke A(1) i (3) (Sl. 9.4 – ) su nestabilni. Druga mogućnost – stabilno stacionarno stanje u kojem je populacija grabežljivaca potpuno izumrla i ostao je samo plijen stabilna tačka 6 ). (3) (Sl. 9.4 (1) – Ovo je posebna tačka
takođe nestabilan čvor. – Konačno, treća mogućnost 9.4 Vodrživi suživot populacija grabežljivaca i plijena (Sl. (9.11).
), čiji su stacionarni brojevi izraženi formulama (9.7) Kao iu slučaju jedne populacije (vidjeti predavanje 3), za modelx 1 , x 2 Moguće je razviti stohastički model, ali on se ne može eksplicitno riješiti. Stoga ćemo se ograničiti na opšta razmatranja. Pretpostavimo, na primjer, da se ravnotežna tačka nalazi na određenoj udaljenosti od svake od osi. Zatim za fazne trajektorije na kojima su vrijednosti
ako ostanu dovoljno veliki, deterministički model će biti sasvim zadovoljavajući. Ali ako u nekom trenutku fazne trajektorije bilo koja varijabla nije velika, onda slučajne fluktuacije mogu postati značajne. Oni dovode do činjenice da se reprezentativna tačka pomiče na jednu od osi, što znači izumiranje odgovarajuće vrste. 1934), Stoga se ispostavlja da je stohastički model nestabilan, jer stohastički "drift" prije ili kasnije dovodi do izumiranja jedne od vrsta. U ovakvom modelu, grabežljivac na kraju izumre, bilo slučajno ili zato što je njegova populacija plijena prvi eliminisana. Stohastički model sistema grabežljivac-plijen dobro objašnjava Gauseove eksperimente (Gause, u kojoj trepavice Paramettum candatum služio kao žrtva za drugu trepetljiku – Didinium nasatum (9.7) predator. Očekivano prema determinističkim jednačinama

ravnotežni brojevi u ovim eksperimentima bili su otprilike samo pet jedinki svake vrste, pa nije iznenađujuće da su u svakom ponovljenom eksperimentu ili grabežljivci ili plijen (a nakon njih i grabežljivci) vrlo brzo izumrli na sl. 9.5.. 9.5. Rice Visina Parametium caudatum i grabežljive trepavice. Dadinium nasutum Od, 1934
Dakle, analiza Volterra modela interakcije vrsta pokazuje da, uprkos širokom spektru tipova ponašanja ovakvih sistema, uopšte ne može postojati neprigušene fluktuacije u broju u modelu konkurentskih vrsta. Međutim, takve oscilacije se uočavaju u prirodi iu eksperimentu. Potreba za njihovim teorijskim objašnjenjem bila je jedan od razloga za formulisanje opisa modela u opštijem obliku.
Generalizovani modeli interakcije dva tipa
Predložen je veliki broj modela za opisivanje interakcije vrsta, čije su desne strane jednadžbe bile funkcije broja populacija u interakciji. Riješeno je pitanje razvoja općih kriterija za utvrđivanje koje vrste funkcija mogu opisati ponašanje privremene veličine populacije, uključujući stabilne fluktuacije. Najpoznatiji od ovih modela pripadaju Kolmogorovu (1935, revidirani članak - 1972) i Rosenzweigu (1963).
 (9.12)
(9.12)
Model uključuje sljedeće pretpostavke:
1) Predatori ne stupaju u interakciju jedni s drugima, tj. stopa reprodukcije predatora k 2 i broj žrtava L istrijebljen u jedinici vremena od strane jednog grabežljivca ne zavisi od y.
2) Povećanje broja plijena u prisustvu grabežljivaca jednako je povećanju odsustva grabežljivaca minus broj plijena kojeg su grabežljivci istrebili. Funkcije k 1 (x), k 2 (x), L(x), su kontinuirani i definirani na pozitivnoj poluosi x, y³ 0.
3) dk 1 /dx< 0. To znači da se stopa reprodukcije plijena u odsustvu grabežljivca monotono smanjuje s povećanjem broja plijena, što odražava ograničenu dostupnost hrane i drugih resursa.
4) dk 2 /dx> 0, k 2 (0) < 0 < k 2 (¥ ). S povećanjem broja plijena, koeficijent reprodukcije grabežljivaca monotono se smanjuje s povećanjem broja plijena, krećući se od negativne vrijednosti, (kada nema šta za jelo) na pozitivno.
5) Broj plijena koji je uništio jedan grabežljivac u jedinici vremena L(x)> 0 at N> 0; L(0)=0.
Mogući tipovi faznih portreta sistema (9.12) prikazani su na Sl. 9.6:

Rice. 9.6.Fazni portreti Kolmogorovljevog sistema (9.12), koji opisuje interakciju dva tipa pri različitim omjerima parametara. Objašnjenja u tekstu.
Stacionarna rješenja (postoje dva ili tri) imaju sljedeće koordinate:
(1). ` x=0;` y=0.
Porijeklo koordinata za bilo koje vrijednosti parametra je sedlo (slika 9.6 a-d).
(2). ` x=A,` y=0.(9.13)
Aodređeno iz jednačine:
k 1 (A)=0.
Stacionarni rješenje (9.13) je sedlo ako B< A (Sl. 9.6 A, b, G), B određeno iz jednačine
k 2 (B)=0
Tačka (9.13) se stavlja u pozitivni kvadrant ako B>A . Ovo je stabilan čvor .
Posljednji slučaj, koji odgovara smrti grabežljivca i preživljavanju plijena, prikazan je na Sl. 9.6 V.
(3). ` x=B,` y=C.(9.14)
Vrijednost C se određuje iz jednačina:
Tačka (9.14) – fokus (Sl.9.6 A) ili čvor (Sl.9.6 G), čija stabilnost zavisi od predznaka veličines
s 2 = – k 1 (B) – k 1 (B)B+L(B)C.
Ako s>0, tačka je stabilna akos<0 ‑ точка неустойчива, и вокруг нее могут существовать предельные циклы (рис. 9.6 b)
U stranoj literaturi se češće razmatra sličan model koji su predložili Rosenzweig i MacArthur (1963):
 (9.15)
(9.15)
Gdje f(x) - stopa promjene broja žrtava x u odsustvu grabežljivaca, F( x,y) - intenzitet predatorstva, k- koeficijent koji karakteriše efikasnost prerade biomase plena u biomasu predatora, e- smrtnost predatora.
Model (9.15) se svodi na poseban slučaj Kolmogorovljevog modela (9.12) pod sljedećim pretpostavkama:
1) broj grabežljivaca je ograničen samo brojem plijena,
2) brzina kojom dati grabežljivac jede plijen ovisi samo o gustini populacije plijena i ne zavisi od gustine populacije grabežljivaca.
Tada jednačine (9.15) poprimaju oblik.

Kada se opisuje interakcija stvarnih vrsta, desna strana jednadžbi je specificirana u skladu sa idejama o biološkim realnostima. Razmotrimo jedan od najpopularnijih modela ove vrste.
Model interakcije između dvije vrste insekata (MacArthur, 1971.)
Model koji ćemo razmotriti u nastavku korišten je za rješavanje praktičnog problema suzbijanja štetnih insekata sterilizacijom mužjaka jedne od vrsta. Na osnovu bioloških karakteristika interakcije vrsta, napisan je sljedeći model
 (9.16)
(9.16)
Evo x,y- biomasa dvije vrste insekata. Trofičke interakcije vrsta opisanih u ovom modelu su vrlo složene. Ovo određuje oblik polinoma na desnoj strani jednadžbe.
Pogledajmo desnu stranu prve jednačine. Vrste insekata X jedu larve vrste at(član +k 3 y), već odrasle osobe vrste at jedu larve vrste X podložni velikoj brojnosti vrsta X ili at ili oba tipa (članovi – k 4 xy, – y 2). At small X smrtnost vrsta X veći od prirodnog priraštaja (1 –k 1 +k 2 x–x 2 < 0 at small X). U drugoj jednačini član k 5 odražava prirodni rast vrste y; –k 6 y – samoograničavanje ovog tipa,–k 7 x– jedenje ličinki vrste at vrste insekata x, k 8 xy – povećanje biomase vrste at zbog konzumiranja odraslih insekata te vrste at larve vrste X.
Na sl. 9.7 (9.16).

Rješenje pitanja kako osigurati suživot populacije sa svojim biološkim okruženjem, naravno, ne može se dobiti bez uzimanja u obzir specifičnosti određenog biološkog sistema i analize svih njegovih međuodnosa. Istovremeno, proučavanje formalnih matematičkih modela omogućava nam da odgovorimo na neka opšta pitanja. Može se tvrditi da za modele kao što je (9.12), činjenica kompatibilnosti ili nekompatibilnosti populacija ne zavisi od njihove početne veličine, već je određena samo prirodom interakcije vrsta. Model pomaže u odgovoru na pitanje: kako utjecati na biocenozu i upravljati njome kako bi se brzo uništile štetne vrste.
Upravljanje se može svesti na kratkoročnu, naglu promjenu vrijednosti stanovništva X I u. Ova metoda odgovara metodama kontrole kao što je jedno uništavanje jedne ili obje populacije hemijskim putem. Iz gore formulisane tvrdnje jasno je da će za kompatibilne populacije ovaj metod kontrole biti neefikasan, jer će vremenom sistem ponovo dostići stacionarni režim.
Drugi način je promjena vrste interakcijskih funkcija između pogleda, na primjer, kada se mijenjaju vrijednosti sistemskih parametara. Ovoj parametarskoj metodi odgovaraju metode biološke kontrole. Dakle, kada se uvedu sterilizirani mužjaci, stopa prirodnog rasta populacije opada. Ako u isto vrijeme dobijemo drugačiju vrstu faznog portreta, onu gdje postoji samo stabilno stacionarno stanje sa nultim brojem štetočina, kontrola će dovesti do željenog rezultata – uništavanje populacije štetne vrste. Zanimljivo je napomenuti da je ponekad preporučljivo primijeniti utjecaj ne na samog štetnika, već na njegovog partnera. Generalno, nemoguće je reći koja je metoda efikasnija. Ovo zavisi od dostupnih kontrola i od eksplicitnog oblika funkcija koje opisuju interakciju populacija.
Model A.D. Bazykin
Teorijska analiza modela interakcija vrsta je najsveobuhvatnije provedena u knjizi A.D. Bazykina "Biofizika međudjelujućih populacija" (M., Nauka, 1985).
Razmotrimo jedan od modela grabežljivac-plijen koji se proučava u ovoj knjizi.
 (9.17)
(9.17)
Sistem (9.17) je generalizacija najjednostavnijeg Volterra modela grabežljivac-plijen (5.17) uzimajući u obzir efekat zasićenja predatora. Model (5.17) pretpostavlja da se intenzitet ispaše plijena linearno povećava sa povećanjem gustine plijena, što ne odgovara stvarnosti pri visokim gustoćama plijena. Različite funkcije mogu se odabrati za opisivanje ovisnosti ishrane grabežljivca o gustoći plijena. Najvažnije je da odabrano funkcionira s rastom x asimptotski teži konstantnoj vrijednosti. Model (9.6) koristi logističku zavisnost. U Bazykinovom modelu, hiperbola je odabrana kao takva funkcija x/(1+px). Podsjetimo da je ovo oblik Monod formule, koja opisuje ovisnost brzine rasta mikroorganizama o koncentraciji supstrata. Ovdje se plijen ponaša kao supstrat, a grabežljivac kao mikroorganizmi. .
Sistem (9.17) zavisi od sedam parametara. Broj parametara se može smanjiti zamjenom varijabli:
x® (A/D)x; y ® (A/D)/y;
t® (1/A)t; g (9,18)
i zavisi od četiri parametra.
Za potpunu kvalitativnu studiju potrebno je četverodimenzionalni prostor parametara podijeliti na područja s različitim tipovima dinamičkog ponašanja, tj. izgraditi parametarski ili strukturalni portret sistema.
Zatim je potrebno konstruisati fazne portrete za svaku od oblasti parametarskog portreta i opisati bifurkacije koje se javljaju kod faznih portreta na granicama različitih oblasti parametarskog portreta.
Konstrukcija kompletnog parametarskog portreta izvodi se u obliku skupa „isječaka“ (projekcija) niskodimenzionalnog parametarskog portreta sa fiksnim vrijednostima nekih od parametara.
Parametarski portret sistema (9.18) za fiksni g i mali e prikazano na slici 9.8. Portret sadrži 10 područja sa različitim tipovima ponašanja faznih putanja.

Rice. 9.8.Parametarski portret sistema (9.18) za fiksnig
i mali e
Ponašanje sistema pri različitim odnosima parametara može biti značajno različito (slika 9.9). Sistem omogućava:
1) jedna stabilna ravnoteža (regije 1 i 5);
2) jedan stabilan granični ciklus (regije 3 i 8);
3) dvije stabilne ravnoteže (regija 2)
4) stabilan granični ciklus i nestabilna ravnoteža unutar njega (regije 6, 7, 9, 10)
5) stabilan granični ciklus i stabilna ravnoteža van njega (regija 4).
U parametarskim regionima 7, 9, 10, oblast privlačnosti ravnoteže je ograničena nestabilnim graničnim ciklusom koji leži unutar stabilnog. Najzanimljivija struktura je fazni portret, koji odgovara oblasti 6 u parametarskom portretu. Detaljno je prikazano na sl. 9.10.

Područje privlačenja ravnoteže B 2 (zasjenjeno) je "puž" koji se uvija iz nestabilnog fokusa B 1. Ako se zna da se u početnom trenutku sistem nalazio u okolini B 1, onda je moguće prosuditi da li će odgovarajuća putanja dostići ravnotežu B 2 ili stabilan granični ciklus koji okružuje tri ravnotežne tačke C (sedlo), B 1 i B 2 na osnovu probabilističkih razmatranja.

Sl.9.10.Fazni portret sistema 9.18 za parametarsko područje 6. Privlačno područje B 2 je zasjenjeno
U parametarskom portretu(9.7) ima 22 razne bifurkacijske granice koje se formiraju 7 razne vrste bifurkacija. Njihovo proučavanje nam omogućava da identifikujemo moguće tipove ponašanja sistema kada se njegovi parametri promene. Na primjer, kada se krećete iz područja 1 do oblasti 3 dolazi do rađanja malog graničnog ciklusa ili mekog rađanja samooscilacija oko jedne ravnoteže IN. Slično meko rađanje samooscilacija, ali oko jedne od ravnoteža, tj. B 1 , javlja se prilikom prelaska granica regiona 2 i 4. Prilikom napuštanja područja 4 do oblasti 5 stabilan granični ciklus oko tačkeB 1 "puca" na petlji separatrica i jedina privlačna tačka ostaje ravnoteža B 2 itd.
Od posebnog interesa za praksu je, naravno, razvoj kriterijuma za blizinu sistema granicama bifurkacije. Zaista, biolozi su itekako svjesni svojstva “tamponiranja” ili “fleksibilnosti” prirodnih ekoloških sistema. Ovi termini se obično odnose na sposobnost sistema da apsorbuje spoljne uticaje. Sve dok intenzitet spoljašnjeg uticaja ne prelazi određenu kritičnu vrednost, ponašanje sistema ne trpi kvalitativne promene. Na faznoj ravni to odgovara povratku sistema u stabilno stanje ravnoteže ili u stabilan granični ciklus, čiji se parametri ne razlikuju mnogo od prvobitnog. Kada intenzitet udara pređe dozvoljeni nivo, sistem se "pokvari" i prelazi u kvalitativno drugačiji način dinamičkog ponašanja, na primjer, jednostavno izumire. Ovaj fenomen odgovara bifurkacijskoj tranziciji.
Svaka vrsta bifurkacijske tranzicije ima svoje karakteristične karakteristike, koje omogućavaju procjenu opasnosti takvog prijelaza za ekosistem. Evo nekih općih kriterija koji ukazuju na blizinu opasne granice. Kao iu slučaju jedne vrste, ako se, kada se broj jedne od vrsta smanji, sistem „zaglavi“ u blizini nestabilnog sedla, što se izražava u vrlo sporom vraćanju broja na početnu vrijednost, tada sistem je blizu kritične granice. Pokazatelj opasnosti je i promjena oblika fluktuacija u broju grabežljivaca i plijena. Ako oscilacije koje su bliske harmonijskim postanu relaksacione, a amplituda oscilacija se povećava, to može dovesti do gubitka stabilnosti sistema i izumiranja jedne od vrsta.
Dalje produbljivanje matematičke teorije interakcije među vrstama ide u pravcu detaljizacije strukture samih populacija i uzimanja u obzir vremenskih i prostornih faktora.
Književnost.
Kolmogorov A.N. Kvalitativno proučavanje matematičkih modela dinamike stanovništva. // Problemi kibernetike. M., 1972, br. 5.
MacArtur R. Grafička analiza ekoloških sistema // Division of biology report Perinceton University. 1971
A.D. Bazykin “Biofizika populacija u interakciji.” M., Nauka, 1985.
V. Volterra: “Matematička teorija borbe za postojanje.” M.. Nauka, 1976
Gause G.F. Borba za egzistenciju. Baltimor, 1934.
Ovdje su, za razliku od (3.2.1), predznaci (-012) i (+a2i) različiti. Kao iu slučaju konkurencije (sistem jednačina (2.2.1)), ishodište koordinata (1) za ovaj sistem je posebna tačka tipa „nestabilan čvor“. Još tri moguća stabilna stanja:

Biološko značenje zahtijeva pozitivne količine X y x 2. Za izraz (3.3.4) to znači da
Ako je koeficijent intraspecifične konkurencije predatora A,22 = 0, uslov (3.3.5) dovodi do uslova ai2
Mogući tipovi faznih portreta za sistem jednačina (3.3.1) prikazani su na Sl. 3.2 a-c. Izokline horizontalnih tangenta su prave linije
a izokline vertikalnih tangenti su prave
Od sl. 3.2 pokazuje sljedeće. Sistem grabežljivac-plijen (3.3.1) može imati stabilnu ravnotežnu poziciju u kojoj je populacija plijena potpuno izumrla (x = 0) i ostali su samo grabežljivci (tačka 2 na slici 3.26). Očigledno, ovakva situacija se može ostvariti samo ako, pored vrste žrtava, X predator X2 ima dodatne izvore napajanja. Ova činjenica se u modelu odražava pozitivnim članom na desnoj strani jednačine za xs. Singularne tačke (1) i (3) (slika 3.26) su nestabilne. Druga mogućnost je stabilno stacionarno stanje, u kojem je populacija grabežljivaca potpuno izumrla i ostao je samo plijen – stabilna tačka (3) (Sl. 3.2a). Ovdje je singularna tačka (1) također nestabilan čvor.
Konačno, treća mogućnost je stabilna koegzistencija populacija predatora i plijena (slika 3.2 c), čiji se stacionarni brojevi izražavaju formulama (3.3.4). Razmotrimo ovaj slučaj detaljnije.
Pretpostavimo da su koeficijenti intraspecifične konkurencije jednaki nuli (ai= 0, i = 1, 2). Pretpostavimo i da se grabežljivci hrane samo plijenom ove vrste X a u njihovom odsustvu odumiru brzinom od C2 (u (3.3.5) C2).
Hajde da izvršimo detaljnu studiju ovog modela, koristeći notaciju koja je najšire prihvaćena u literaturi. Refurbishment

Rice. 3.2. Lokacija glavnih izoklina na faznom portretu Volterra sistema predator-plijen za različite omjere parametara: A- o -
WITH I C2 C2
1, 3 - nestabilna, 2 - stabilna singularna tačka; V -
1, 2, 3 - nestabilna, 4 - stabilna singularna tačka značajna
Sistem grabežljivac-plijen u ovim notacijama ima oblik:

Proučavaćemo svojstva rješenja sistema (3.3.6) na faznoj ravni N1
ON2
Sistem ima dva stacionarna rješenja. Oni se mogu lako odrediti izjednačavanjem desne strane sistema sa nulom. dobijamo: 
Otuda stacionarna rješenja:

Pogledajmo pobliže drugo rješenje. Nađimo prvi integral sistema (3.3.6) koji ne sadrži t. Pomnožimo prvu jednačinu sa -72, drugu sa -71 i dodajmo rezultate. dobijamo:
Podijelimo sada prvu jednačinu sa N i pomnoži sa € 2, a drugu podijelite sa JV 2 i pomnožite sa e. Dodajmo još jednom rezultate:
Upoređujući (3.3.7) i (3.3.8), imaćemo:

Integracijom dobijamo:

Ovo je željeni prvi integral. Dakle, sistem (3.3.6) je konzervativan jer ima prvi integral kretanja, veličinu koja je funkcija sistemskih varijabli N I N2 i nezavisno od vremena. Ovo svojstvo nam omogućava da za Volterra sisteme konstruišemo sistem koncepata sličan statističkoj mehanici (vidi Poglavlje 5), gde energetska vrednost sistema, koja je konstantna u vremenu, igra značajnu ulogu.
Za svaki fiksni od > 0 (što odgovara određenim početnim podacima), integral odgovara određenoj putanji na ravni N1 ON2 , koji služi kao putanja sistema (3.3.6).
Razmotrimo grafičku metodu konstruisanja putanje, koju je predložio sam Volterra. Imajte na umu da desna strana formule (3.3.9) zavisi samo od D g 2, a leva samo od N. Označimo
Iz (3.3.9) slijedi da između X I Y postoji proporcionalni odnos
Na sl. 3.3 prikazuje prve kvadrante četiri koordinatna sistema XOY, NOY, N2 OX i D G 1 0N2 tako da svi imaju zajedničko poreklo.
U gornjem lijevom uglu (kvadrant NOY) grafik funkcije (3.3.8) je iscrtan u donjem desnom uglu (kvadrant N2 VOL)- graf funkcije Y. Prva funkcija ima min at Ni = a drugi - max at N2 = ?-
Konačno, u kvadrantu XOY konstruirajmo pravu liniju (3.3.12) za neke fiksne WITH.
Hajde da označimo tačku N na osi ON. Ova tačka odgovara određenoj vrijednosti Y(N 1), što je lako pronaći crtanjem okomice

Rice. 3.3.
kroz N dok se ne ukrsti sa krivom (3.3.10) (vidi sliku 3.3). Zauzvrat, vrijednost K(D^) odgovara određenoj tački M na pravoj Y = cX a samim tim i neku vrednost X(N) = Y(N)/c, koji se može naći crtanjem okomica A.M. I M.D. Pronađena vrijednost (ova tačka je na slici označena slovom D) dve tačke odgovaraju R I G na krivulji (3.3.11). Koristeći ove tačke, crtajući okomite, naći ćemo dvije tačke odjednom E" I E", koji leže na krivulji (3.3.9). Njihove koordinate:

Crtanje okomice A.M., prešli smo krivu (3.3.10) u još jednoj tački IN. Ova tačka odgovara istoj R I Q na krivulji (3.3.11) i isto N I SCH. Koordinate N ova tačka se može naći ispuštanjem okomice iz IN po osi ON. Tako da dobijamo bodove F" i F", također leži na krivulji (3.3.9).
Dolazi sa druge tačke N, na isti način dobijamo nove četiri tačke koje leže na krivulji (3.3.9). Izuzetak će biti poenta Ni= ?2/72- Na osnovu toga dobijamo samo dva boda: TO I L. To će biti donja i gornja tačka krive (3.3.9).
Ne može se krenuti od vrijednosti N, i iz vrijednosti N2 . Idemo iz N2 do krive (3.3.11), zatim se diže do prave Y = cX, a odatle prelazeći krivu (3.3.10), nalazimo i četiri tačke krive (3.3.9). Izuzetak će biti poenta Ne=?1/71- Na osnovu toga dobijamo samo dva boda: G I TO. To će biti krajnje lijeve i krajnje desne tačke krivulje (3.3.9). Pitajući drugačije N I N2 i nakon što smo dobili dosta tačaka, povezujući ih, približno ćemo konstruisati krivulju (3.3.9).
Iz konstrukcije je jasno da je to zatvorena kriva koja u sebi sadrži tačku 12 = (?2/721?1/71)” počevši od određenih početnih podataka N Yu i N20. Uzimajući drugu vrijednost C, tj. drugim početnim podacima, dobijamo još jednu zatvorenu krivu koja ne seče prvu i takođe sadrži tačku (?2/721 ?1/71)1 unutar sebe. Dakle, porodica putanja (3.3.9) je porodica zatvorenih linija koje okružuju tačku 12 (vidi sliku 3.3). Proučimo vrstu stabilnosti ove singularne tačke pomoću metode Ljapunova.
Pošto su svi parametri e 1, ?2, 71,72 su pozitivni, tačka (N[ se nalazi u pozitivnom kvadrantu fazne ravni. Linearizacija sistema blizu ove tačke daje:

Evo n(t) i 7i2(N1, N2 :
Karakteristična jednačina sistema (3.3.13):

Korijeni ove jednadžbe su čisto imaginarni:

Dakle, proučavanje sistema pokazuje da su putanje u blizini singularne tačke predstavljene koncentričnim elipsama, a sama singularna tačka je centar (slika 3.4). Volterra model koji se razmatra takođe ima zatvorene putanje daleko od singularne tačke, iako je oblik ovih putanja već drugačiji od elipsoidnog. Ponašanje varijabli Ni, N2 tokom vremena prikazano je na sl. 3.5.

Rice. 3.4.

Rice. 3.5. Ovisnost broja plijena N ja i grabežljivac N2 s vremena na vrijeme
Singularna tačka centralnog tipa je stabilna, ali ne asimptotski. Pokažimo na ovom primjeru šta je to. Pusti oklevanje Ni(t) i LGgM se javljaju na način da se reprezentativna tačka kreće duž fazne ravni duž putanje 1 (vidi sliku 3.4). U trenutku kada je tačka u poziciji M, u sistem se dodaje određeni broj individua izvana N 2, tako da predstavlja tačka skače sa tačke M do tačke A/". Nakon toga, ako je sistem opet prepušten sam sebi, oscilacije Ni I N2 već će se dešavati sa većim amplitudama nego ranije, a reprezentativna tačka se kreće duž putanje 2. To znači da su oscilacije u sistemu nestabilne: one zauvek menjaju svoje karakteristike pod spoljnim uticajem. U budućnosti ćemo razmatrati modele koji opisuju stabilne oscilatorne režime i pokazuju da se na faznoj ravni takva asimptotska stabilna periodična kretanja opisuju korištenjem graničnih ciklusa.
Na sl. Na slici 3.6 prikazane su eksperimentalne krive - fluktuacije u broju krznarskih životinja u Kanadi (prema kompaniji Hudson's Bay). Ove krive su konstruisane na osnovu podataka o broju ubranih koža. Periodi fluktuacije u broju zečeva (plijena) i risova (predatora) su približno isti i kreću se od 9-10 godina. U ovom slučaju, maksimalni broj zečeva je, po pravilu, ispred maksimalnog broja risova za jednu godinu.
Oblik ovih eksperimentalnih krivulja je mnogo manje pravilan od teorijskih. Međutim, u ovom slučaju je dovoljno da model osigura podudarnost najznačajnijih karakteristika teorijske i eksperimentalne krive, tj. vrijednosti amplitude i fazni pomaci između fluktuacija u broju grabežljivaca i plijena. Mnogo ozbiljniji nedostatak Volterra modela je nestabilnost rješenja sistema jednačina. Zaista, kao što je gore spomenuto, svaka nasumična promjena u brojnosti jedne ili druge vrste trebala bi, slijedeći model, dovesti do promjene amplitude oscilacija obje vrste. Naravno, u prirodni usloviživotinje su podvrgnute bezbrojnim takvim slučajnim uticajima. Kao što se može vidjeti iz eksperimentalnih krivulja, amplituda fluktuacija u broju vrsta malo varira iz godine u godinu.
Volterra model je referentni (osnovni) za matematičku ekologiju u istoj mjeri u kojoj je model harmonijskog oscilatora osnovni za klasičnu i kvantnu mehaniku. Koristeći ovaj model, zasnovan na vrlo pojednostavljenim idejama o prirodi obrazaca koji opisuju ponašanje sistema, čisto matematički
Poglavlje 3

Rice. 3.6. Kinetičke krivulje broja krznenih životinja prema podacima krznarske kompanije Hudson Bay (Seton-Thomson, 1987.) Na osnovu zaključka izvedena je kvalitativnost ponašanja takvog sistema - o prisutnosti fluktuacije stanovništva u takvom sistemu. Bez konstruisanja matematičkog modela i njegovog korišćenja, takav zaključak bi bio nemoguć.
U onome o čemu smo raspravljali gore u jednostavnom obliku Volterra sistem ima dva fundamentalna i međusobno povezana nedostatka. Njihovom „eliminisanju“ posvećena je opsežna ekološka i matematička literatura. Prvo, uključivanje bilo kojih dodatnih faktora, ma koliko malih, u model kvalitativno mijenja ponašanje sistema. Drugi "biološki" nedostatak modela je da ne uključuje fundamentalna svojstva svojstvena bilo kojem paru populacija koje djeluju u skladu s principom grabežljivca i plijena: učinak zasićenja grabežljivca, ograničene resurse grabežljivca i plijena čak i sa viškom plijena, mogućnost minimalnog broja plijena na raspolaganju za predatora itd.
Da bi se ovi nedostaci otklonili, predlagali su različiti autori razne modifikacije Volterra sistemi. O najzanimljivijim od njih biće reči u odeljku 3.5. Ovdje ćemo se fokusirati samo na model koji uzima u obzir samoograničenja u rastu obje populacije. Primjer ovog modela jasno pokazuje kako se priroda odluka može promijeniti kada se promijene sistemski parametri.
Dakle, razmatramo sistem

Sistem (3.3.15) se razlikuje od prethodno razmatranog sistema (3.3.6) po prisustvu članova oblika -7 na desnoj strani jednačine uNf,
Ovi pojmovi odražavaju činjenicu da populacija plijena ne može rasti beskonačno čak ni u odsustvu grabežljivaca zbog ograničenih resursa hrane i ograničenog staništa. Ista "samoograničenja" nametnuta su populaciji predatora.
Pronaći stacionarne brojeve vrsta iVi i N2 Izjednačimo desnu stranu jednačina sistema (3.3.15) sa nulom. Rešenja sa nultim brojem grabežljivaca ili plena nas sada neće zanimati. Stoga, razmotrite algebarski sistem
jednačine  Njena odluka
Njena odluka
daje nam koordinate singularne tačke. Ovdje treba nametnuti uslov pozitivnosti stacionarnih brojeva na parametre sistema: N> 0 i N2 > 0. Korijeni karakteristične jednadžbe sistema lineariziranog u blizini singularne tačke (3.3.16):

Iz izraza za karakteristične brojeve jasno je da ako je uslov ispunjen
Tada broj grabežljivaca i plijena prolazi kroz prigušene oscilacije tokom vremena, sistem ima singularnu tačku različitu od nule i stabilan fokus. Fazni portret takvog sistema prikazan je na Sl. 3.7 a.
Pretpostavimo da parametri u nejednakosti (3.3.17) mijenjaju svoje vrijednosti na način da uvjet (3.3.17) postaje jednakost. Tada su karakteristični brojevi sistema (3.3.15) jednaki, a njegova singularna tačka će ležati na granici između regiona stabilnih žarišta i čvorova. Kada se predznak nejednakosti (3.3.17) obrne, singularna tačka postaje stabilan čvor. Fazni portret sistema za ovaj slučaj prikazan je na Sl. 3.76.
Kao iu slučaju jedne populacije, za model (3.3.6) može se razviti stohastički model, ali se za njega ne može dobiti eksplicitno rješenje. Stoga ćemo se ograničiti na opšta razmatranja. Pretpostavimo, na primjer, da se ravnotežna tačka nalazi na određenoj udaljenosti od svake od osi. Zatim za fazne trajektorije na kojima su vrijednosti JVj, N2 ako ostanu dovoljno veliki, deterministički model će biti sasvim zadovoljavajući. Ali ako u nekom trenutku


Rice. 3.7. Fazni portret sistema (3.3.15): A - kada je odnos (3.3.17) između parametara zadovoljen; b- kada se izvodi inverzni odnos između parametara
fazna trajektorija, bilo koja varijabla nije velika, onda slučajne fluktuacije mogu postati značajne. Oni dovode do činjenice da se reprezentativna tačka pomiče na jednu od osi, što znači izumiranje odgovarajuće vrste. Stoga se ispostavlja da je stohastički model nestabilan, jer stohastički "drift" prije ili kasnije dovodi do izumiranja jedne od vrsta. U ovakvom modelu, grabežljivac na kraju izumre, bilo slučajno ili zato što je njegova populacija plijena prvi eliminisana. Stohastički model sistema grabežljivac-plijen dobro objašnjava eksperimente Gausea (Gause, 1934; 2000), u kojima trepavice u kojoj trepavice služio kao žrtva za drugu trepetljiku služio kao žrtva za drugu trepetljiku- predator. Očekivani ravnotežni brojevi prema determinističkim jednadžbama (3.3.6) u ovim eksperimentima bili su otprilike samo pet jedinki svake vrste, pa nije iznenađujuće da su u svakom ponovljenom eksperimentu ili grabežljivci ili plijen vrlo brzo izumrli (a potom i grabežljivci) .
Dakle, analiza Volterra modela interakcije vrsta pokazuje da, uprkos širokom spektru tipova ponašanja ovakvih sistema, uopšte ne može postojati neprigušene fluktuacije u broju u modelu konkurentskih vrsta. U modelu grabežljivac-plijen, neprigušene oscilacije pojavljuju se kao rezultat izbora poseban obrazac jednačine modela (3.3.6). U ovom slučaju, model postaje negrub, što ukazuje na nepostojanje u takvom sistemu mehanizama koji žele da očuvaju njegovo stanje. Međutim, takve oscilacije se uočavaju u prirodi i eksperimentu. Potreba za njihovim teorijskim objašnjenjem poslužila je kao jedan od razloga za formulisanje opisa modela u više opšti pogled. Odjeljak 3.5 posvećen je razmatranju takvih generaliziranih modela.
PA88 sistem, koji istovremeno predviđa vjerovatnoću više od 100 farmakoloških efekata i mehanizama djelovanja supstance na osnovu njene strukturne formule. Efikasnost ovakvog pristupa planiranju skrininga je oko 800%, a tačnost kompjuterske prognoze je 300% veća od predviđanja stručnjaka.
Dakle, jedan od konstruktivnih alata za sticanje novih znanja i rješenja u medicini je metoda matematičkog modeliranja. Proces matematizacije medicine je česta manifestacija međuprožimanja naučna saznanja, povećanje efikasnosti tretmana i preventivnog rada.
4. Matematički model “predator-plijen”
Po prvi put u biologiji, matematički model periodičnih promjena u broju antagonističkih životinjskih vrsta predložio je talijanski matematičar V. Volterra i njegove kolege. Model koji je predložio Volterra bio je razvoj ideje koju je 1924. iznio A. Lottka u knjizi “Elementi fizičke biologije”. Stoga je ovaj klasični matematički model poznat kao “Lottky-Volterra” model.
Iako su u prirodi odnosi antagonističkih vrsta složeniji nego u modelu, oni su ipak dobar nastavni model na kojem se proučavaju osnovne ideje matematičkog modeliranja.
Dakle, problem: u nekom ekološki zatvorenom području žive dvije vrste životinja (na primjer, risovi i zečevi). Zečevi (plijen) se hrane biljnom hranom, koja je uvijek dostupna u dovoljnim količinama (ovaj model ne uzima u obzir ograničene resurse biljna hrana). Risovi (predatori) mogu jesti samo zečeve. Potrebno je utvrditi kako će se broj plijena i grabežljivaca mijenjati s vremenom u takvom ekološki sistem. Ako se populacija plijena povećava, povećava se vjerojatnost susreta između grabežljivaca i plijena, te se, shodno tome, nakon određenog vremenskog kašnjenja povećava populacija grabežljivaca. Ovaj prilično jednostavan model sasvim adekvatno opisuje interakciju između stvarnih populacija grabežljivaca i plijena u prirodi.
Hajdemo sada sastavljanje diferencijalnih jednadžbi. O
označimo broj plijena sa N, a broj predatora sa M. Brojevi N i M su funkcije vremena t. U našem modelu uzimamo u obzir sljedeće faktore:
a) prirodna reprodukcija žrtava; b) prirodna smrt žrtava;
c) uništavanje žrtava tako što ih pojedu grabežljivci; d) prirodno izumiranje predatora;
e) povećanje broja predatora zbog razmnožavanja u prisustvu hrane.
Jer mi pričamo o tome o matematičkom modelu, zadatak je dobiti jednačine koje bi uključivale sve predviđene faktore i koje bi opisale dinamiku, odnosno promjenu broja predatora i plijena tokom vremena.
Neka se broj plijena i grabežljivaca promijeni za ∆N i ∆M tokom nekog vremena t. Promjena broja žrtava ∆N tokom vremena ∆t određena je, prvo, povećanjem kao rezultatom prirodne reprodukcije (koje je proporcionalno dostupnom broju žrtava):
gdje je B koeficijent proporcionalnosti koji karakterizira stopu prirodnog izumiranja žrtava.
Izvođenje jednadžbe koja opisuje smanjenje broja plijena zbog njihove konzumacije od strane grabežljivaca zasniva se na ideji da što se češće susreću, to se broj plijena brže smanjuje. Također je jasno da je učestalost susreta između grabežljivaca i plijena proporcionalna i broju žrtava i broju grabežljivaca, tada
Dijeljenjem lijeve i desne strane jednačine (4) sa ∆t i prelaskom na granicu na ∆t→0, dobijamo diferencijalnu jednačinu prvog reda:
Da biste riješili ovu jednačinu, morate znati kako se broj predatora (M) mijenja tokom vremena. Promjena broja grabežljivaca (∆M) određena je povećanjem zbog prirodnog razmnožavanja u prisustvu dovoljno hrane (M 1 = Q∙N∙M∙∆t) i smanjenjem zbog prirodnog izumiranja predatora ( M 2 = - P∙M∙∆ t):
M = Q∙N∙M∙∆t - P∙M∙∆t |
Iz jednačine (6) možemo dobiti diferencijalnu jednačinu:
Diferencijalne jednadžbe (5) i (7) predstavljaju matematički model “predator-plijen”. Dovoljno je odrediti vrijednosti koeficijenta

Za rješavanje problema mogu se koristiti enti A, B, C, Q, P i matematički model.
Provjera i podešavanje matematičkog modela. U ovoj laboratoriji
Pored izračunavanja najkompletnijeg matematičkog modela (jednačine 5 i 7), predlaže se proučavanje jednostavnijih u kojima se nešto ne uzima u obzir.
Uzimajući u obzir pet nivoa složenosti matematičkog modela, možete "osjetiti" fazu provjere i prilagođavanja modela.
1. nivo – u modelu se uzima u obzir samo njihova prirodna reprodukcija za “plijen”, nema “predatora”;
Nivo 2 – model uzima u obzir prirodno izumiranje “plijena”, nema “predatora”;
Nivo 3 – model uzima u obzir prirodnu reprodukciju “žrtva”
I izumiranje, bez “predatora”;
4. nivo – model uzima u obzir prirodnu reprodukciju “žrtva”
I izumiranje, kao i da ih pojedu „predatori“, ali broj „predatora“ ostaje nepromijenjen;
Nivo 5 – model uzima u obzir sve faktore o kojima se raspravlja.
Dakle, imamo sledeći sistem diferencijalnih jednačina:
gdje je M broj “predatora”; N – broj “žrtva”;
t – trenutno vrijeme;
A – stopa reprodukcije “žrtava”; C – učestalost susreta grabežljivca i plijena; B – stopa izumiranja “žrtava”;
Q – reprodukcija “predatora”;
P – izumiranje “predatora”.
1. nivo: M = 0, B = 0; 2. nivo: M = 0, A = 0; 3. nivo: M = 0; 4. nivo: Q = 0, P = 0;
5. nivo: kompletan sistem jednačine.
Zamjenom vrijednosti koeficijenata u svaki nivo, dobit ćemo različita rješenja, na primjer:
Za 3. nivo vrijednost koeficijenta M=0, tada

rješavajući jednačinu koju dobijamo
Isto tako za nivoe 1 i 2. Što se tiče 4. i 5. nivoa, ovdje je potrebno riješiti sistem jednačina Runge-Kutta metodom. Kao rezultat, dobijamo rješenje za matematičke modele ovih nivoa.
II. RAD UČENIKA TOKOM PRAKTIČNE NASTAVE
Zadatak 1. Kontrola usmenog govora i korekcija savladavanja teorijskog gradiva časa. Prolazni prijem na časove.
Zadatak 2. Izvođenje laboratorijskih radova, diskusija o dobijenim rezultatima, pisanje bilješki.
Obavljanje posla
1. Sa radne površine računara pozovite program „Laboratorija br. 6“ tako što ćete dvaput kliknuti na odgovarajuću prečicu levim tasterom miša.
2. Dvaput kliknite lijevu tipku miša na prečicu "PREDATOR".
3. Odaberite prečicu "PRED" i ponovite poziv programa lijevom tipkom miša (dvostrukim klikom).
4. Nakon naslovnog ekrana, pritisnite "ENTER".
5. Modeliranje počinje sa 1. nivo.
6. Unesite godinu od koje će se model analizirati: na primjer, 2000
7. Odaberite vremenske intervale, na primjer, unutar 40 godina, nakon 1 godine (zatim nakon 4 godine).
2. nivo: B = 0,05; N0 = 200;
3. nivo: A = 0,02; B = 0,05; N = 200;
4. nivo: A = 0,01; B = 0,002; C = 0,01; N0 = 200; M = 40; 5. nivo: A = 1; B = 0,5; C = 0,02; Q = 0,002; P = 0,3; N0 = 200;
9. Pripremiti pisani izvještaj o radu koji treba da sadrži jednačine, grafikone, rezultate proračuna karakteristika modela, zaključke o obavljenom radu.
Zadatak 3. Praćenje konačnog nivoa znanja:
a) usmeni izvještaj o obavljenom laboratorijskom radu; b) rješavanje situacijskih problema; c) kompjutersko testiranje.
Zadatak 4. Zadatak za sljedeću lekciju: dio i tema časa, koordinacija tema za apstraktne izvještaje (obim izvještaja 2-3 stranice, vremensko ograničenje 5-7 minuta).
Još 20-ih godina. A. Lotka, a nešto kasnije, nezavisno od njega, predložen je V. Voltaire matematički modeli, opisujući povezane fluktuacije u obilju predatora i plijena.
Model se sastoji od dvije komponente:
C – broj predatora; N – broj žrtava;
Pretpostavimo da će u odsustvu grabežljivaca populacija plijena rasti eksponencijalno: dN/dt = rN. Ali grabežljivac uništavaju plijen brzinom koja je određena učestalošću susreta između grabežljivca i plijena, a učestalost susreta raste kako se povećava broj grabežljivaca (C) i plijena (N). Tačan broj naiđenog i uspješno pojedenog plijena ovisit će o efikasnosti kojom grabežljivac pronađe i uhvati plijen, tj. od a’ – “efikasnost pretraživanja” ili “učestalost napada”. Dakle, učestalost „uspješnih“ susreta između grabežljivca i plijena, a samim tim i stopa jedenja žrtava bit će jednaka a’SN i općenito: dN/dt = rN – a’CN (1*).
U nedostatku hrane, pojedinačni grabežljivci gube na težini, gladuju i umiru. Pretpostavimo da će se u modelu koji razmatramo veličina populacije grabežljivca u nedostatku hrane zbog gladovanja eksponencijalno smanjiti: dC/dt = - qC, gdje je q mortalitet. Smrt se nadoknađuje rođenjem novih pojedinaca po stopi za koju se vjeruje da u ovom modelu ovisi o dvije okolnosti:
1) stopa potrošnje hrane, a’CN;
2) efikasnost (f) kojom ova hrana prelazi u potomstvo predatora.
Dakle, plodnost grabežljivca jednaka je fa’CN i općenito: dC/dt = fa’CN – qC (2*). Jednačine 1* i 2* čine Lotka-Wolterov model. Mogu se proučavati svojstva ovog modela, konstruirati izokline linija koje odgovaraju konstantnoj veličini populacije i uz pomoć takvih izoklina može se odrediti ponašanje populacija grabežljivaca i plijena u interakciji.
U slučaju populacije plijena: dN/dt = 0, rN = a’CN, ili C = r/a’. Jer r i a’ = const, izoklina za žrtvu će biti linija za koju je vrijednost C konstantna:
Kod male gustine grabežljivaca (C), broj plijena (N) se povećava, naprotiv, smanjuje se.
Slično za predatore (jednačina 2*) sa dC/dt = 0, fa’CN = qC, ili N = q/fa’, tj. Izoklina za grabežljivca će biti linija duž koje je N konstantan: pri velikoj gustoći plijena, populacija predatora se povećava, a pri niskoj gustoći smanjuje.
Njihov broj prolazi kroz neograničene konjugirane fluktuacije. Kada je broj plijena veliki, broj grabežljivaca se povećava, što dovodi do povećanja pritiska grabežljivaca na populaciju plijena, a time i do smanjenja njenog broja. Ovo smanjenje, pak, dovodi do ograničenja grabežljivaca u hrani i pada njihovog broja, što uzrokuje slabljenje pritiska grabežljivaca i povećanje broja plijena, što opet dovodi do povećanja populacije grabežljivaca. , itd.
Populacije obavljaju isti ciklus oscilacija neograničeno dugo dok im neki vanjski utjecaj ne promijeni brojnost, nakon čega populacije izvode nove cikluse neograničenih oscilacija. Zapravo, okruženje se stalno mijenja, a veličina populacije će se stalno mijenjati novi nivo. Da bi ciklusi oscilacija koje populacija čini bili pravilni, oni moraju biti stabilni: ako vanjski utjecaj mijenja nivo populacije, onda moraju težiti izvornom ciklusu. Takvi ciklusi se nazivaju stabilni, granični ciklusi.
Lotka-Wolterov model nam omogućava da pokažemo glavni trend u odnosu grabežljivac-plijen, koji se izražava u pojavi fluktuacija u populaciji plijena, praćenih fluktuacijama u populaciji grabežljivca. Glavni mehanizam takvih fluktuacija je vremensko kašnjenje svojstveno slijedu stanja od velikog broja plijena do velikog broja grabežljivaca, zatim do malog broja plijena i malog broja grabežljivaca, do velikog broja plijena, itd.
5) POPULACIJSKE STRATEGIJE PREDATORA I PRIMATA
Odnos “predator-plijen” predstavlja karike u procesu prijenosa materije i energije od fitofaga u zoofage ili od grabežljivaca nižeg reda do predatora. višeg reda. By Na osnovu prirode ovih odnosa razlikuju se tri vrste grabežljivaca:
A) sakupljači. Predator prikuplja male, prilično brojne pokretne žrtve. Ova vrsta grabežljivca je tipična za mnoge vrste ptica (zjeba, zeba, šipak, itd.), koje troše energiju samo na traženje žrtava;
b) pravi predatori. Predator vreba i ubija plijen;
V) stočari. Ovi grabežljivci više puta koriste plijen, na primjer, gadflies ili konjske muhe.
Strategija dobivanja hrane kod grabežljivaca usmjerena je na osiguravanje energetske efikasnosti prehrane: potrošnja energije za dobivanje hrane trebala bi biti manja od energije dobivene tijekom njene asimilacije.
Pravi predatori se dijele na
"žeteoci" koji se hrane obilnim resursima (uključujući planktonsku ribu, pa čak i kitove baletane), i "lovce" koji traže manje obilnu hranu. Zauzvrat
“Lovci” se dijele na “zasjede” koji čekaju plijen (na primjer, štuka, jastreb, mačka, bogomoljka), “tragače” (ptice insektojede) i “progonitelje”. Za posljednju grupu traženje hrane nije potrebno visoki troškovi energije, ali je potrebno mnogo da preuzme žrtvu (lavovi u savanama). Međutim, neki grabežljivci mogu kombinirati elemente strategije različite opcije lov.
Kao iu odnosu "fitofag-biljka", situacija u kojoj sve žrtve pojedu grabežljivci, što na kraju dovodi do njihove smrti, nije uočena u prirodi. Ekološka ravnoteža između grabežljivaca i plijena se održava specijalni mehanizmi , smanjujući rizik od potpunog istrebljenja žrtava. Dakle, žrtve mogu:
Bježi od predatora. U ovom slučaju, kao rezultat adaptacija, povećava se mobilnost i žrtava i grabežljivaca, što je posebno tipično za stepske životinje koje se nemaju gdje sakriti od svojih progonitelja;
Steknite zaštitnu boju („pretvarajte se“ da su lišće ili grančice) ili, naprotiv, svijetlu boju, N.: crvenu, upozoravajući grabežljivca na gorak okus. Poznato je da se boja zeca mijenja različita vremena godine, što mu omogućava da se ljeti kamuflira u travi, a zimi u pozadini bijeli snijeg. Adaptivne promjene boje mogu se pojaviti u različitim fazama ontogeneze: mladunci tuljana su bijeli (boja snijega), a odrasli su crni (boja kamenite obale);
Distribuirati u grupama, što čini njihovo traženje i hvatanje energetski intenzivnijim za predatora;
Sakrij se u skloništa;
Pređite na mjere aktivne odbrane (biljojedi s rogovima, bodljikave ribe), ponekad zglobne (mošusni volovi mogu zauzeti “ svestrana odbrana„od vukova itd.).
Zauzvrat, grabežljivci razvijaju ne samo sposobnost brzog progona plijena, već i čulo mirisa, što im omogućava da po mirisu odrede lokaciju plijena. Mnoge vrste grabežljivaca rasturaju jame svojim žrtvama (lisice, vukovi).
Istovremeno, oni sami čine sve da izbjegnu otkrivanje njihovog prisustva. To objašnjava čistoću malih mačaka, koje provode dosta vremena u toaletu i zakopavanju izmeta kako bi uklonile mirise. Predatori nose „maskirne haljine“ (pruge štuka i smuđova, što ih čini manje uočljivim u šikarama makrofita, prugama tigrova itd.).
Potpuna zaštita od grabežljivaca svih jedinki u populacijama grabljivica također ne dolazi, jer bi to dovelo ne samo do smrti izgladnjelih grabežljivaca, već u konačnici i do katastrofe populacija plijena. Istovremeno, u nedostatku ili smanjenju gustine naseljenosti grabežljivaca, genetski fond populacije plijena se pogoršava (zadržavaju se bolesne i stare životinje) i zbog naglo povećanje njihov broj potkopava opskrba hranom.
Iz tog razloga, efekt ovisnosti veličine populacije plijena i grabežljivaca - pulsiranje veličine populacije plijena, praćeno pulsiranjem veličine populacije grabežljivaca s određenim zakašnjenjem („Lotka-Volterra efekt“) - rijetko se opaža .
Uspostavljen je prilično stabilan omjer između biomase predatora i plijena. Tako R. Ricklefs daje podatke da se omjer biomase predatora i plijena kreće od 1:150 do 1:300. U različitim ekosistemima umjerena zona SAD za jednog vuka ima 300 malih belorepanih jelena (težine 60 kg), 100 veliki jelen wapiti (težina 300 kg) ili 30 losova (težina 350). Isti obrazac je pronađen u savanama.
Uz intenzivnu eksploataciju populacija fitofaga, ljudi često isključuju grabežljivce iz ekosistema (u Velikoj Britaniji, na primjer, ima srndaća i jelena, ali nema vukova; u umjetnim akumulacijama gdje se uzgajaju šaran i druge ribnjačke ribe, nema štuka). U ovom slučaju, ulogu grabežljivca obavlja sama osoba, uklanjajući dio jedinki populacije fitofaga.
Posebna varijanta grabežljivosti uočena je kod biljaka i gljiva. U biljnom carstvu postoji oko 500 vrsta koje su sposobne uhvatiti insekte i djelomično ih probaviti uz pomoć proteolitičkih enzima. Predatorske pečurke formiraju uređaje za hvatanje u obliku malih ovalnih ili sferičnih glava smještenih na kratkim granama micelija. Međutim, najčešći tip zamke su ljepljive trodimenzionalne mreže koje se sastoje od veliki broj prstenovi nastali kao rezultat grananja hifa. Predatorske gljive mogu uhvatiti prilično velike životinje, poput okruglih crva. Nakon što se crv uplete u hife, one rastu unutar tijela životinje i brzo ga ispunjavaju.
1.Stalni i povoljni nivoi temperature i vlažnosti.
2. Obilje hrane.
3.Zaštita od nepovoljnih faktora.
4.Agresivan hemijski sastav stanište (probavni sokovi).
1. Prisustvo dva staništa: okruženje prvog reda je organizam domaćin, okruženje drugog reda je spoljašnja sredina.
