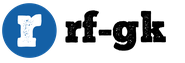O ecuație exponențială cu baze diferite. Putere sau ecuații exponențiale

În această lecție, ne vom uita la rezolvarea mai complexă ecuații exponențiale, să reamintim principalele prevederi teoretice referitoare la funcția exponențială.

1. Definiția și proprietățile unei funcții exponențiale, o tehnică de rezolvare a celor mai simple ecuații exponențiale

Amintiți-vă definiția și principalele proprietăți ale unei funcții exponențiale. Soluția tuturor ecuațiilor și inegalităților exponențiale se bazează pe proprietăți.

Functie exponentiala este o funcție de forma , unde baza este gradul și Aici x este o variabilă independentă, un argument; y - variabilă dependentă, funcție.

Orez. 1. Graficul funcției exponențiale

Graficul arată un exponent crescător și descrescător, ilustrând funcția exponențială de la bază mai mare decât unulși, respectiv, mai mic de unu, dar mai mare decât zero.

Ambele curbe trec prin punctul (0;1)

Proprietățile funcției exponențiale:

Domeniu: ;

Interval de valori: ;

Funcția este monotonă, crește cu , scade cu .

O funcție monotonă ia fiecare dintre valorile sale cu o singură valoare a argumentului.

Când argumentul crește de la minus la plus infinit, funcția crește de la zero, inclusiv, la plus infinit. Dimpotrivă, când argumentul crește de la minus la plus infinit, funcția scade de la infinit la zero, inclusiv.

2. Rezolvarea ecuațiilor exponențiale tipice

Amintiți-vă cum să rezolvați cele mai simple ecuații exponențiale. Soluția lor se bazează pe monotonitatea funcției exponențiale. Aproape toate ecuațiile exponențiale complexe sunt reduse la astfel de ecuații.

Egalitatea exponenților la temeiuri egale datorita proprietatii functiei exponentiale si anume monotonitatii acesteia.

Metoda de rezolvare:

Echivalează bazele gradelor;

Echivalează exponenți.

Să trecem la ecuații exponențiale mai complexe, scopul nostru este să reducem fiecare dintre ele la cele mai simple.

Să scăpăm de rădăcina din partea stângă și să reducem gradele la aceeași bază:

Pentru a reduce o ecuație exponențială complexă la una simplă, este adesea folosită o schimbare de variabile.

Să folosim proprietatea gradului:

Introducem un înlocuitor. Să , atunci . Cu o astfel de înlocuire, este evident că y ia strict valori pozitive. Primim:

Înmulțim ecuația rezultată cu doi și transferăm toți termenii în partea stângă:

Prima rădăcină nu satisface intervalul de valori y, o aruncăm. Primim:

Să aducem gradele la același indicator:

Introducem un înlocuitor:

Lasă atunci . Cu această înlocuire, este evident că y ia valori strict pozitive. Primim:

Știm cum să rezolvăm ecuații pătratice similare, scriem răspunsul:

Pentru a vă asigura că rădăcinile sunt găsite corect, puteți verifica conform teoremei Vieta, adică găsiți suma rădăcinilor și produsul lor și verificați cu coeficienții corespunzători ai ecuației.

Primim:

3. Tehnica de rezolvare a ecuaţiilor exponenţiale omogene de gradul II

Să studiem următorul tip important de ecuații exponențiale:

Ecuațiile de acest tip se numesc omogene de gradul doi în raport cu funcțiile f și g. Pe partea stângă se află un trinom pătrat față de f cu parametrul g sau un trinom pătrat față de g cu parametrul f.

Metoda de rezolvare:

Această ecuație poate fi rezolvată ca una pătratică, dar este mai ușor să o faci invers. Trebuie luate în considerare două cazuri:

În primul caz, obținem

În al doilea caz, avem dreptul de a împărți cu cel mai înalt grad și obținem:

Ar trebui să introducem o schimbare de variabile, obținem ecuație pătratică cu privire la:

Rețineți că funcțiile f și g pot fi arbitrare, dar ne interesează cazul în care acestea sunt funcții exponențiale.

4. Exemple de rezolvare a ecuațiilor omogene

Să mutăm toți termenii în partea stângă a ecuației:

Deoarece funcțiile exponențiale capătă valori strict pozitive, avem dreptul de a împărți imediat ecuația la , fără a lua în considerare cazul când:

Primim:

Introducem un înlocuitor: (conform proprietăților funcției exponențiale)

Avem o ecuație pătratică:

Determinăm rădăcinile conform teoremei Vieta:

Prima rădăcină nu satisface intervalul de valori y, o aruncăm, obținem:

Să folosim proprietățile gradului și să reducem toate gradele la baze simple:

Este ușor de observat funcțiile f și g:

Deoarece funcțiile exponențiale capătă valori strict pozitive, avem dreptul de a împărți imediat ecuația la , fără a lua în considerare cazul când .

În etapa de pregătire pentru proba finală, elevii de liceu trebuie să-și îmbunătățească cunoștințele pe tema „Ecuații exponențiale”. Experiența anilor trecuți indică faptul că astfel de sarcini provoacă anumite dificultăți pentru școlari. Prin urmare, elevii de liceu, indiferent de nivelul lor de pregătire, trebuie să stăpânească cu atenție teoria, să memoreze formulele și să înțeleagă principiul rezolvării unor astfel de ecuații. După ce au învățat să facă față acestui tip de sarcini, absolvenții vor putea conta pe scoruri mari cu promovarea examenului matematică.

Pregătește-te pentru examenul împreună cu Shkolkovo!

La repetarea materialelor parcurse, mulți elevi se confruntă cu problema găsirii formulelor necesare rezolvării ecuațiilor. Un manual școlar nu este întotdeauna la îndemână, iar selecția informațiilor necesare pe o temă de pe Internet durează mult.

Portalul educațional Shkolkovo invită studenții să folosească baza noastră de cunoștințe. Implementăm complet metoda noua pregătirea pentru proba finală. Studiind pe site-ul nostru, vei putea identifica lacunele în cunoștințe și vei fi atent tocmai acelor sarcini care provoacă cele mai mari dificultăți.

Profesorii de la „Șkolkovo” au adunat, sistematizat și prezentat tot ce este necesar pentru livrare cu succes UTILIZAȚI materialîn cel mai simplu și accesibil mod.

Principalele definiții și formule sunt prezentate în secțiunea „Referință teoretică”.

Pentru o mai bună asimilare a materialului, vă recomandăm să exersați temele. Revizuiți cu atenție exemplele de ecuații exponențiale cu soluții prezentate pe această pagină pentru a înțelege algoritmul de calcul. După aceea, continuați cu sarcinile din secțiunea „Cataloguri”. Puteți începe cu cele mai ușoare sarcini sau puteți merge direct la rezolvarea ecuațiilor exponențiale complexe cu mai multe necunoscute sau . Baza de date de exerciții de pe site-ul nostru este completată și actualizată în mod constant.

Acele exemple cu indicatori care ți-au cauzat dificultăți pot fi adăugate la „Favorite”. Așa că le puteți găsi rapid și puteți discuta soluția cu profesorul.

Pentru a trece cu succes examenul, studiați pe portalul Shkolkovo în fiecare zi!

Ce este o ecuație exponențială? Exemple.

Deci, o ecuație exponențială... O nouă expoziție unică la expoziția noastră generală cu o mare varietate de ecuații!) Așa cum este aproape întotdeauna cazul, cuvântul cheie al oricărui termen matematic nou este adjectivul corespunzător care îl caracterizează. Deci și aici. cuvânt cheieîn termenul „ecuație exponențială” este cuvântul "demonstrativ". Ce înseamnă? Acest cuvânt înseamnă că necunoscutul (x) este în termeni de orice grad.Și numai acolo! Acest lucru este extrem de important.

De exemplu, aceste ecuații simple:

3 x +1 = 81

5x + 5x +2 = 130

4 2 2 x -17 2 x +4 = 0

Sau chiar acești monștri:

2 sin x = 0,5

Vă rog să acordați imediat atenție unui lucru important: în temeiuri grade (de jos) - doar numere. Dar în indicatori grade (sus) - o mare varietate de expresii cu x. Absolut oricare.) Totul depinde de ecuația specifică. Dacă, brusc, x iese în ecuație în altă parte, în plus față de indicator (să zicem, 3 x \u003d 18 + x 2), atunci o astfel de ecuație va fi deja o ecuație tip mixt. Astfel de ecuații nu au reguli clare de rezolvare. Prin urmare, în această lecție nu le vom lua în considerare. Spre bucuria elevilor.) Aici vom lua în considerare doar ecuaţiile exponenţiale în formă „pură”.

În general, chiar și ecuațiile exponențiale pure nu sunt rezolvate clar în toate cazurile și nu întotdeauna. Dar, printre varietatea bogată de ecuații exponențiale, există anumite tipuri care pot și ar trebui rezolvate. Aceste tipuri de ecuații sunt pe care le vom lua în considerare împreună cu dvs. Și cu siguranță vom rezolva exemplele.) Așa că ne instalăm confortabil și - la drum! Ca și în „împușcăturile” pe computer, călătoria noastră va trece prin niveluri.) De la elementar la simplu, de la simplu la mediu și de la mediu la complex. Pe parcurs, veți aștepta și un nivel secret - trucuri și metode de rezolvare a exemplelor non-standard. Cele despre care nu vei citi în majoritatea manualelor școlare... Ei bine, la final, desigur, șeful final te așteaptă sub formă de teme.)

Nivelul 0. Care este cea mai simplă ecuație exponențială? Rezolvarea celor mai simple ecuații exponențiale.

Pentru început, să ne uităm la unele elementare sincere. Trebuie să începi de undeva, nu? De exemplu, această ecuație:

2 x = 2 2

Chiar și fără teorii, prin logică simplă și bun simț este clar că x = 2. Nu există altă cale, nu? Nicio altă valoare a lui x nu este bună... Acum să ne îndreptăm atenția asupra dosar de decizie această ecuație exponențială grozavă:

2 x = 2 2

X = 2

Ce s-a întâmplat cu noi? Și s-au întâmplat următoarele. Noi, de fapt, am luat și... doar am aruncat aceleași baze (doi)! Complet aruncat afară. Și, ce dorește, lovește-te în ochi!

Da, într-adevăr, dacă în ecuația exponențială din stânga și dreapta sunt aceeași numere în orice grad, atunci aceste numere pot fi aruncate și pur și simplu echivalează exponenții. Matematica permite.) Și apoi puteți lucra separat cu indicatori și puteți rezolva o ecuație mult mai simplă. E grozav, nu?

Iată ideea cheie de a rezolva orice ecuație exponențială (da, exact oricare!): prin intermediul transformări identice este necesar să se asigure că stânga și dreapta din ecuație sunt aceeași numere de bază în diferite grade. Și apoi puteți elimina în siguranță aceleași baze și echivalați exponenții. Și lucrați cu o ecuație mai simplă.

Și acum ne amintim de regula de fier: este posibil să se elimine aceleași baze dacă și numai dacă în ecuația din stânga și din dreapta numerele de bază sunt în singurătate mândră.

Ce înseamnă, într-o izolare splendidă? Aceasta înseamnă fără vecini și coeficienți. Explic.

De exemplu, în ecuație

3 3 x-5 = 3 2 x +1

Nu poți elimina tripleții! De ce? Pentru că în stânga nu avem doar un singur trei în grad, dar muncă 3 3 x-5 . O triplă în plus iese în cale: un coeficient, înțelegi.)

Același lucru se poate spune despre ecuație

5 3 x = 5 2 x +5 x

Și aici, toate bazele sunt aceleași - cinci. Dar în dreapta nu avem un singur grad de cinci: există suma gradelor!

Pe scurt, avem dreptul de a elimina aceleași baze numai atunci când ecuația noastră exponențială arată așa și doar așa:

Af (X) = a g (X)

Acest tip de ecuație exponențială se numește cel mai simplu. Sau stiintific, canonic . Și indiferent care ar fi ecuația răsucită din fața noastră, într-un fel sau altul, o vom reduce la o formă atât de simplă (canonică). Sau, în unele cazuri, să agregate ecuații de acest fel. Atunci cea mai simplă ecuație a noastră poate fi în vedere generala rescrie asa:

F(x) = g(x)

Si asta e. Aceasta va fi transformarea echivalentă. În același timp, absolut orice expresie cu x poate fi folosită ca f(x) și g(x). Tot ceea ce.

Poate că un student deosebit de curios se va întreba: de ce naiba aruncăm atât de ușor și pur și simplu aceleași baze din stânga și din dreapta și echivalăm exponenții? Intuiția este intuiție, dar dintr-o dată, într-o ecuație și dintr-un motiv oarecare, această abordare se va dovedi greșită? Este întotdeauna legal să arunci aceleași baze? Din nefericire, pentru un răspuns matematic riguros la această întrebare interesantă, trebuie să ne scufundăm destul de profund și serios în teorie generală comportamentul dispozitivului și al funcției. Și puțin mai precis - în fenomen monotonitate strictă.În special, monotonitatea strictă functie exponentialay= un x. Deoarece funcția exponențială și proprietățile ei sunt cele care stau la baza soluției ecuațiilor exponențiale, da.) Un răspuns detaliat la această întrebare va fi dat într-o lecție specială separată dedicată rezolvării ecuațiilor complexe non-standard folosind monotonitatea diferitelor funcții.)

A explica acest punct în detaliu acum înseamnă doar să scoți creierul unui școlar obișnuit și să-l sperii din timp cu o teorie seacă și grea. nu voi face asta.) Pentru principalul nostru acest moment sarcina - invata sa rezolvi ecuatii exponentiale! Cel mai simplu! Prin urmare, până transpiram și aruncăm cu îndrăzneală aceleași motive. Aceasta este poate sa, credeți-mă pe cuvânt!) Și apoi rezolvăm deja ecuația echivalentă f (x) = g (x). De regulă, este mai simplu decât exponențialul original.

Se presupune, desigur, că oamenii știu deja să rezolve cel puțin , iar ecuațiile, deja fără x în indicatori.) Cine încă nu știe cum, nu ezitați să închideți această pagină, să parcurgeți linkurile corespunzătoare și să completați vechile goluri. Altfel, îți va fi greu, da...

Tac în privința ecuațiilor iraționale, trigonometrice și a altor ecuații brutale care pot apărea și în procesul de eliminare a bazelor. Dar nu vă alarmați, deocamdată nu vom lua în considerare staniul sincer din punct de vedere al grade: este prea devreme. Ne vom antrena doar pe cele mai simple ecuații.)

Acum luați în considerare ecuațiile care necesită un efort suplimentar pentru a le reduce la cele mai simple. Pentru a le distinge, să le numim ecuații exponențiale simple. Deci, să trecem la următorul nivel!

Nivelul 1. Ecuații exponențiale simple. Recunoaște grade! indicatori naturali.

Regulile cheie în rezolvarea oricăror ecuații exponențiale sunt reguli de abordare a diplomelor. Fără aceste cunoștințe și abilități, nimic nu va funcționa. Vai. Deci, dacă sunt probleme cu diplomele, atunci pentru început ești binevenit. În plus, avem nevoie și de . Aceste transformări (până la două!) stau la baza rezolvării tuturor ecuațiilor matematicii în general. Și nu doar vitrine. Așa că, cine a uitat, faceți o plimbare și pe link: le-am pus cu un motiv.

Dar numai acțiunile cu puteri și transformări identice nu sunt suficiente. De asemenea, necesită observație personală și ingeniozitate. Avem nevoie de aceleași temeiuri, nu-i așa? Așa că examinăm exemplul și le căutăm într-o formă explicită sau deghizată!

De exemplu, această ecuație:

3 2x – 27x +2 = 0

Prima privire la temeiuri. Sunt diferite! Trei și douăzeci și șapte. Dar este prea devreme pentru a intra în panică și a cădea în disperare. Este timpul să ne amintim asta

27 = 3 3

Numerele 3 și 27 sunt rude în grad! Mai mult, rude.) Prin urmare, avem tot dreptul să scriem:

27 x +2 = (3 3) x+2

Și acum ne conectăm cunoștințele despre acţiuni cu grade(si te-am avertizat!). Există o formulă atât de utilă:

(am) n = a mn

Acum, dacă îl rulați în curs, în general se dovedește bine:

27 x +2 = (3 3) x+2 = 3 3(x +2)

Exemplul original arată acum astfel:

3 2 x – 3 3(x +2) = 0

Super, bazele gradelor s-au aliniat. Pentru ce ne străduiam. Jumătate din treabă este gata.) Și acum lansăm transformarea de bază a identității - transferăm 3 3 (x +2) la dreapta. Nimeni nu a anulat acțiunile elementare ale matematicii, da.) Obținem:

3 2 x = 3 3(x +2)

Ce ne oferă acest tip de ecuație? Și faptul că acum ecuația noastră este redusă la forma canonică: în stânga și în dreapta sunt aceleași numere (triple) în puteri. Și ambii tripleți - într-o izolare splendidă. Îndepărtăm cu îndrăzneală tripleții și obținem:

2x = 3(x+2)

Rezolvăm asta și obținem:

X=-6

Cam despre asta e. Acesta este răspunsul corect.)

Și acum înțelegem cursul deciziei. Ce ne-a salvat în acest exemplu? Am fost salvați de cunoașterea gradelor tripluului. Cum anume? Noi identificat numărul 27 criptat trei! Acest truc (codificarea aceleiași baze sub numere diferite) este unul dintre cele mai populare în ecuațiile exponențiale! Doar dacă nu este cel mai popular. Da, și de asemenea, apropo. De aceea, observația și capacitatea de a recunoaște puterile altor numere în numere sunt atât de importante în ecuațiile exponențiale!

Sfaturi practice:

Trebuie să cunoașteți puterile numerelor populare. In fata!

Desigur, oricine poate ridica doi la puterea a șaptea sau trei la a cincea. Nu în mintea mea, deci cel puțin pe o schiță. Dar în ecuațiile exponențiale, este mult mai des necesar să nu se ridice la o putere, ci, dimpotrivă, să se afle ce număr și în ce măsură se ascunde în spatele numărului, să zicem, 128 sau 243. Și asta este deja mai mult complicat decât simpla exponențiere, vezi. Simțiți diferența, așa cum se spune!

Deoarece capacitatea de a recunoaște grade pe față este utilă nu numai la acest nivel, ci și la următoarele, iată o mică sarcină pentru tine:

Stabiliți ce puteri și ce numere sunt numere:

4; 8; 16; 27; 32; 36; 49; 64; 81; 100; 125; 128; 216; 243; 256; 343; 512; 625; 729; 1024.

Răspunsuri (împrăștiate, desigur):

27 2 ; 2 10 ; 3 6 ; 7 2 ; 2 6 ; 9 2 ; 3 4 ; 4 3 ; 10 2 ; 2 5 ; 3 5 ; 7 3 ; 16 2 ; 2 7 ; 5 3 ; 2 8 ; 6 2 ; 3 3 ; 2 9 ; 2 4 ; 2 2 ; 4 5 ; 25 2 ; 4 4 ; 6 3 ; 8 2 ; 9 3 .

Da Da! Nu fi surprins că există mai multe răspunsuri decât sarcini. De exemplu, 2 8 , 4 4 și 16 2 sunt toate 256.

Nivelul 2. Ecuații exponențiale simple. Recunoaște grade! Exponenți negativi și fracționari.

La acest nivel, folosim deja cunoștințele noastre despre grade la maximum. Și anume, implicăm indicatori negativi și fracționali în acest proces fascinant! Da Da! Trebuie să creștem puterea, nu?

De exemplu, această ecuație teribilă:

Din nou, mai întâi uitați-vă la fundații. Bazele sunt diferite! Și de data asta nici pe departe prieten asemanator pe un prieten! 5 și 0,04... Și pentru a elimina bazele, sunt necesare aceleași... Ce să faci?

E bine! De fapt, totul este la fel, doar conexiunea dintre cele cinci și 0,04 este puțin vizibilă vizual. Cum ieșim? Și să trecem la numărul 0,04 la fracție obișnuită! Și acolo, vedeți, totul este format.)

0,04 = 4/100 = 1/25

Wow! Se pare că 0,04 este 1/25! Ei bine, cine ar fi crezut!)

Ei bine, cum? Acum legătura dintre numerele 5 și 1/25 este mai ușor de văzut? Asta e...

Și acum, conform regulilor de operațiuni cu puteri cu indicator negativ poate fi scris cu mâna fermă:

Asta este grozav. Așa că am ajuns la aceeași bază - cinci. Înlocuim acum numărul incomod 0,04 din ecuație cu 5 -2 și obținem:

Din nou, conform regulilor de operare cu puteri, acum putem scrie:

(5 -2) x -1 = 5 -2(x -1)

Pentru orice eventualitate, vă reamintesc (deodată, cine nu știe) că regulile de bază pentru acțiunile cu grade sunt valabile pentru orice indicatori! Inclusiv pentru cele negative.) Așa că nu ezitați să luați și să înmulțiți indicatorii (-2) și (x-1) conform regulii corespunzătoare. Ecuația noastră devine din ce în ce mai bună:

Tot! Pe lângă cei cinci singuratici din grade din stânga și dreapta, nu mai este nimic altceva. Ecuația este redusă la formă canonică. Și apoi - de-a lungul pistei moletate. Înlăturăm cincisele și echivalăm indicatorii:

X 2 –6 X+5=-2(X-1)

Exemplul este aproape gata. Matematica elementară a claselor de mijloc rămâne - deschidem (corect!) Parantezele și colectăm totul din stânga:

X 2 –6 X+5 = -2 X+2

X 2 –4 X+3 = 0

Rezolvăm asta și obținem două rădăcini:

X 1 = 1; X 2 = 3

Asta e tot.)

Acum să ne gândim din nou. În acest exemplu, a trebuit din nou să recunoaștem același număr în grade diferite! Și anume, pentru a vedea cinci criptați în numărul 0,04. Și de data aceasta, în grad negativ! Cum am făcut-o? În mișcare - în niciun caz. Dar după trecerea de la fracție zecimală 0,04 la fracția ordinară 1/25 totul a fost evidențiat! Și apoi întreaga decizie a mers ca un ceas.)

Prin urmare, un alt sfat practic verde.

Dacă există fracții zecimale în ecuația exponențială, atunci trecem de la fracții zecimale la cele obișnuite. LA fracții comune este mult mai ușor să recunoști puterile multor numere populare! După recunoaștere, trecem de la fracții la puteri cu exponenți negativi.

Rețineți că o astfel de simulare în ecuațiile exponențiale apare foarte, foarte des! Și persoana nu este în subiect. Se uită, de exemplu, la numerele 32 și 0,125 și se supără. Nu-i știe că acesta este același doi, doar în grade diferite... Dar ești deja în subiect!)

Rezolvați ecuația:

În! Pare o groază liniștită... Cu toate acestea, aparențele sunt înșelătoare. Aceasta este cea mai simplă ecuație exponențială, în ciuda faptului că este terifiantă aspect. Și acum ți-o arăt.)

În primul rând, ne ocupăm de toate numerele care se află în baze și în coeficienți. Evident că sunt diferiți, da. Dar totuși ne asumăm riscul și încercăm să le facem aceeași! Să încercăm să ajungem la același număr în grade diferite. Și, de preferință, numărul cât mai mic posibil. Deci, să începem descifrarea!

Ei bine, totul este clar cu cele patru deodată - este 2 2 . Deci, deja ceva.)

Cu o fracțiune de 0,25 - nu este încă clar. Trebuie verificat. Folosim sfaturi practice - treceți de la zecimal la obișnuit:

0,25 = 25/100 = 1/4

Deja mult mai bine. Deocamdată este deja clar că 1/4 este 2 -2. Grozav, iar numărul 0,25 este, de asemenea, asemănător cu un doi.)

Până acum, bine. Dar cel mai rău număr dintre toate rămâne - rădăcina pătrată a doi! Ce să faci cu acest ardei? Poate fi reprezentată și ca o putere a doi? Si cine stie...

Ei bine, din nou urcăm în tezaurul nostru de cunoștințe despre diplome! De data aceasta, ne conectăm în plus cunoștințele despre rădăcini. De la cursul clasei a IX-a, tu și cu mine a trebuit să înduram că orice rădăcină, dacă se dorește, poate fi întotdeauna transformată într-un grad cu o fracție.

Ca aceasta:

În cazul nostru:

Cum! Se pare că rădăcina pătrată a lui doi este 2 1/2. Asta e!

E in regula! Toate numerele noastre incomode s-au dovedit de fapt a fi un doi criptat.) Nu mă cert, undeva criptat foarte sofisticat. Dar ne creștem și profesionalismul în rezolvarea unor astfel de cifruri! Și atunci totul este deja evident. Înlocuim numerele 4, 0,25 și rădăcina lui doi din ecuația noastră cu o putere a lui doi:

Tot! Bazele tuturor gradelor din exemplu au devenit aceleași - două. Și acum sunt folosite acțiunile standard cu grade:

a mun n = a m + n

a m:a n = a m-n

(am) n = a mn

Pentru partea stângă obțineți:

2 -2 (2 2) 5 x -16 = 2 -2+2(5 x -16)

Pentru partea dreaptă va fi:

Și acum ecuația noastră rea a început să arate așa:

Pentru cei care nu și-au dat seama cum exact a rezultat această ecuație, atunci întrebarea nu este despre ecuațiile exponențiale. Întrebarea este despre acțiuni cu puteri. Am rugat urgent sa repet celor care au probleme!

Iată linia de sosire! Primit vedere canonică ecuație exponențială! Ei bine, cum? Te-am convins că nu este atât de înfricoșător? ;) Îndepărtăm doi și echivalăm indicatorii:

Rămâne doar să rezolvăm această ecuație liniară. Cum? Cu ajutorul transformărilor identice, desigur.) Rezolvați ceea ce este deja acolo! Înmulțiți ambele părți cu două (pentru a elimina fracția 3/2), mutați termenii cu X-uri la stânga, fără X-uri la dreapta, aduceți asemenea, numărați - și veți fi fericit!

Totul ar trebui să iasă frumos:

X=4

Acum să ne regândim decizia. În acest exemplu, am fost salvați de tranziția de la rădăcină pătrată la grad cu exponent 1/2. Mai mult, doar o astfel de transformare vicleană ne-a ajutat pretutindeni să ajungem la aceeași bază (deuce), care a salvat situația! Și, dacă nu ar fi, atunci am avea toate șansele să înghețăm pentru totdeauna și să nu facem față niciodată acestui exemplu, da...

Prin urmare, nu neglijăm următorul sfat practic:

Dacă există rădăcini în ecuația exponențială, atunci trecem de la rădăcini la puteri cu exponenți fracționari. De foarte multe ori, doar o astfel de transformare clarifică situația ulterioară.

Desigur, gradele negative și fracționale sunt deja mult mai complicate decât gradele naturale. Cel puțin în ceea ce privește percepția vizuală și, mai ales, recunoașterea de la dreapta la stânga!

Este clar că ridicarea directă, de exemplu, a unui doi la puterea lui -3 sau a unui patru la puterea lui -3/2 nu este o problemă atât de mare. Pentru cei care știu.)

Dar du-te, de exemplu, realizează imediat asta

0,125 = 2 -3

Sau

Aici doar practica și experiența bogată regulă, da. Și, desigur, o vedere clară, Ce este un exponent negativ și un exponent fracționar. Precum și - sfaturi practice! Da, da, acelea verde.) Sper că, totuși, vă vor ajuta să navigați mai bine în toată varietatea pestriță de grade și să vă creșteți semnificativ șansele de succes! Deci să nu le neglijăm. nu sunt degeaba în verde scriu uneori.)

Pe de altă parte, dacă devii „tu” chiar și cu puteri exotice precum negative și fracționale, atunci posibilitățile tale de rezolvare a ecuațiilor exponențiale se vor extinde enorm și vei fi deja capabil să gestionezi aproape orice tip de ecuații exponențiale. Ei bine, dacă nu oricare, atunci 80 la sută din toate ecuațiile exponențiale - cu siguranță! Da, da, nu glumesc!

Așadar, prima noastră parte de cunoaștere a ecuațiilor exponențiale a ajuns la concluzia sa logică. Și, ca antrenament intermediar, sugerez în mod tradițional să rezolvi puțin pe cont propriu.)

Exercitiul 1.

Pentru ca cuvintele mele despre descifrarea gradelor negative și fracționale să nu fie în zadar, îmi propun să joc un mic joc!

Exprimați numărul ca putere a doi:

Răspunsuri (în dezordine):

S-a întâmplat? Amenda! Apoi facem o misiune de luptă - rezolvăm cele mai simple și simple ecuații exponențiale!

Sarcina 2.

Rezolvați ecuații (toate răspunsurile sunt o mizerie!):

5 2x-8 = 25

2 5x-4 – 16x+3 = 0

Raspunsuri:

x=16

X 1 = -1; X 2 = 2

X = 5

S-a întâmplat? Într-adevăr, mult mai ușor!

Apoi rezolvăm următorul joc:

(2 x +4) x -3 = 0,5 x 4 x -4

35 1-x = 0,2 - x 7 x

Raspunsuri:

X 1 = -2; X 2 = 2

X = 0,5

X 1 = 3; X 2 = 5

Și aceste exemple de unul au rămas? Amenda! Crești! Apoi, iată câteva exemple pe care să le gustați:

Raspunsuri:

X = 6

X = 13/31

X = -0,75

X 1 = 1; X 2 = 8/3

Și s-a hotărât? Ei bine, respect! îmi scot pălăria.) Deci, lecția nu a fost în zadar și Primul nivel rezolvarea ecuațiilor exponențiale poate fi considerată stăpânită cu succes. Înainte - nivelurile următoareși altele ecuații complexe! Și noi tehnici și abordări. Și exemple non-standard. Și noi surprize.) Toate acestea - în lecția următoare!

Ceva nu a mers? Deci, cel mai probabil, problemele sunt în . Sau în . Sau ambele în același timp. Aici sunt neputincios. Poate in inca o data oferiți un singur lucru - nu fi leneș și faceți o plimbare prin linkuri.)

Va urma.)

Universitatea de Stat din Belgorod

SCAUN algebră, teoria numerelor și geometrie

Tema de lucru: Ecuații și inegalități exponențiale-putere.

Munca de absolvent student al Facultății de Fizică și Matematică

supraveghetor:

______________________________

Revizor: ________________________________

________________________

Belgorod. 2006

Introducere			3
Subiect eu.	Analiza literaturii de specialitate pe tema de cercetare.
Subiect II.	Funcțiile și proprietățile lor utilizate în rezolvarea ecuațiilor și inegalităților de putere exponențială.
	I.1.	Funcția de putereși proprietățile sale.
	I.2.	Funcția exponențială și proprietățile ei.
Subiect III.	Rezolvarea ecuațiilor de putere exponențială, algoritm și exemple.
Subiect IV.	Rezolvarea inegalităților exponențiale-putere, plan de soluție și exemple.
Subiect v.	Experiență în conducerea cursurilor cu școlari pe tema: „Rezolvarea ecuațiilor și inegalităților exponențiale-putere”.
v. 1.	Material didactic.
v. 2.	Sarcini pentru soluție independentă.
Concluzie.	Concluzii si oferte.
Bibliografie.
Aplicații

Introducere.

„... bucuria de a vedea și înțelege...”

A. Einstein.

În această lucrare, am încercat să transmit experiența mea de profesor de matematică, să transmit, cel puțin într-o oarecare măsură, atitudinea mea față de predarea ei - o chestiune umană în care știința matematică, pedagogia, didactica, psihologia și chiar filosofia sunt surprinzător. împletite.

Am avut ocazia să lucrez cu copii și absolvenți, cu copii care stau la polii dezvoltării intelectuale: cei care erau înscriși la psihiatru și care erau cu adevărat interesați de matematică.

Am rezolvat multe sarcini metodologice. Voi încerca să vorbesc despre cele pe care am reușit să le rezolv. Dar și mai mult - nu a fost posibil, iar în cele care par a fi rezolvate apar noi întrebări.

Dar și mai importante decât experiența în sine sunt reflecțiile și îndoielile profesorului: de ce este exact așa, această experiență?

Iar vara este diferită acum, iar rândul educației a devenit mai interesant. „Sub Jupiteri” astăzi nu este căutarea unui sistem optim mitic de predare „toată lumea și totul”, ci copilul însuși. Dar apoi – cu necesitate – și profesorul.

LA curs şcolar algebră și începutul analizei, clasele 10 - 11, la promovarea examenului la curs liceu iar la examenele de admitere la universități există ecuații și inegalități care conțin necunoscutul la bază și exponenți - sunt ecuații și inegalități exponențiale-putere.

Li se acordă puțină atenție la școală, practic nu există sarcini pe această temă în manuale. Totuși, stăpânirea metodologiei de rezolvare a acestora, mi se pare, este foarte utilă: crește abilitățile mentale și creative ale elevilor, ni se deschid orizonturi complet noi. La rezolvarea problemelor, elevii dobândesc primele deprinderi muncă de cercetare, cultura lor matematică este îmbogățită, capacitatea lor de a gandire logica. Elevii dezvoltă astfel de trăsături de personalitate precum intenția, stabilirea de obiective, independența, care le vor fi utile în viața ulterioară. Și, de asemenea, există o repetare, extindere și asimilare profundă a materialului educațional.

Am început să lucrez la acest subiect din cercetarea tezei mele cu scrierea unei lucrări de termen. În cursul căreia am studiat și analizat mai aprofundat literatura de specialitate pe această temă, am identificat cea mai potrivită metodă de rezolvare a ecuațiilor și inegalităților exponențiale-putere.

Constă în faptul că, pe lângă abordarea general acceptată la rezolvarea ecuațiilor de putere exponențială (baza se ia mai mare decât 0) și la rezolvarea acelorași inegalități (baza se consideră mai mare decât 1 sau mai mare decât 0, dar mai mică decât 1), sunt luate în considerare și cazurile când bazele sunt negative, sunt 0 și 1.

Analiza scrisa lucrări de examen elevii arată că necunoașterea problemei de valoare negativă argumentul funcţiei exponenţiale în manualele școlare, le provoacă o serie de dificultăți și duce la apariția unor erori. Și, de asemenea, au probleme la etapa de sistematizare a rezultatelor obținute, unde, din cauza trecerii la ecuație - o consecință sau inegalitate - o consecință, pot apărea rădăcini străine. Pentru a elimina erorile, folosim o verificare a ecuației sau inegalității inițiale și un algoritm pentru rezolvarea ecuațiilor de putere exponențială sau un plan pentru rezolvarea inegalităților de putere exponențială.

Pentru ca studenții să-și treacă cu succes absolvirea și examene de admitere, cred că este necesar să acordăm mai multă atenție rezolvării ecuațiilor și inegalităților exponențiale-putere în clasă, sau suplimentar la opțiuni și cercuri.

Prin urmare subiect , Ale mele teza se definește astfel: „Ecuații și inegalități exponențiale-putere”.

Goluri lucrarea prezentă sunteți:

1. Analizați literatura pe această temă.

2. Oferiți o analiză completă a soluției ecuațiilor și inegalităților exponențiale-putere.

3. Dați un număr suficient de exemple pe această temă de diferite tipuri.

4. Verificați la lecție, orele opționale și în cerc modul în care vor fi percepute metodele propuse pentru rezolvarea ecuațiilor și inegalităților exponențiale-putere. Oferiți recomandări adecvate pentru studiul acestui subiect.

Subiect cercetarea noastră este de a dezvolta o tehnică de rezolvare a ecuațiilor și inegalităților exponențiale de putere.

Scopul și subiectul studiului au necesitat rezolvarea următoarelor sarcini:

1. Studiați literatura de specialitate pe tema: „Ecuații și inegalități exponențiale-putere”.

2. Stăpânește metodele de rezolvare a ecuațiilor și inegalităților exponențiale-putere.

3. Selectați materialul de instruire și dezvoltați un sistem de exerciții la diferite niveluri pe tema: „Rezolvarea ecuațiilor și inegalităților exponențiale-putere”.

În cadrul cercetării de diplomă au fost analizate peste 20 de lucrări, dedicate aplicării diferitelor metode de rezolvare a ecuațiilor și inegalităților exponențiale-putere. De aici ajungem.

Planul tezei:

Introducere.

Capitolul I. Analiza literaturii de specialitate pe tema de cercetare.

Capitolul II. Funcțiile și proprietățile lor utilizate în rezolvarea ecuațiilor și inegalităților de putere exponențială.

II.1. Funcția de putere și proprietățile acesteia.

II.2. Funcția exponențială și proprietățile ei.

Capitolul III. Rezolvarea ecuațiilor de putere exponențială, algoritm și exemple.

Capitolul IV. Rezolvarea inegalităților exponențiale-putere, plan de soluție și exemple.

Capitolul V. Experiență în conducerea cursurilor cu școlari pe această temă.

1. Material educativ.

2. Sarcini pentru soluție independentă.

Concluzie. Concluzii si oferte.

Lista literaturii folosite.

Literatura analizată în capitolul I

1º. ecuații exponențiale denumește ecuațiile care conțin o variabilă în exponent.

Rezolvarea ecuațiilor exponențiale se bazează pe proprietatea puterii: două puteri cu aceeași bază sunt egale dacă și numai dacă exponenții lor sunt egali.

2º. Modalități de bază de rezolvare a ecuațiilor exponențiale:

1) cea mai simplă ecuație are o soluție;

2) o ecuație de formă prin logaritm la bază A adus aminte;

3) ecuația formei este echivalentă cu ecuația ;

4) o ecuație de formă este echivalentă cu ecuația.

5) o ecuație de formă printr-o înlocuire se reduce la o ecuație, iar apoi se rezolvă o mulțime de ecuații exponențiale cele mai simple;

6) ecuație cu mărimi reciproce prin înlocuire reduceți la ecuație și apoi rezolvați setul de ecuații;

7) ecuaţii omogene în raport cu a g(x)și b g (x) dat fiind drăguț prin substituție se reduce la ecuație și apoi se rezolvă setul de ecuații.

Clasificarea ecuațiilor exponențiale.

1. Ecuații rezolvate prin tranziție la o bază.

Exemplul 18. Rezolvați ecuația .

Rezolvare: Să profităm de faptul că toate bazele puterilor sunt puteri a lui 5: .

2. Ecuații rezolvate prin trecerea la un exponent.

Aceste ecuații sunt rezolvate prin transformarea ecuației inițiale în forma , care se reduce la cel mai simplu folosind proprietatea proporției.

Exemplul 19. Rezolvați ecuația:

3. Ecuații rezolvate prin bracketing factorul comun.

Dacă în ecuație fiecare exponent diferă de celălalt printr-un anumit număr, atunci ecuațiile se rezolvă prin paranteze gradul cu cel mai mic exponent.

Exemplul 20. Rezolvați ecuația.

Soluție: Să punem gradul cu cel mai mic exponent din paranteze din partea stângă a ecuației:

Exemplul 21. Rezolvați ecuația

Rezolvare: Grupăm separat în partea stângă a ecuației termenii care conțin grade cu baza 4, în partea dreaptă - cu baza 3, apoi punem din paranteze gradele cu cel mai mic exponent:

4. Ecuații care se reduc la ecuații pătratice (sau cubice)..

Următoarele ecuații sunt reduse la o ecuație pătratică în raport cu noua variabilă y:

a) tipul de substituție , în timp ce ;

b) tipul de substituire , în timp ce .

Exemplul 22. Rezolvați ecuația .

Rezolvare: Să facem o schimbare de variabilă și să rezolvăm ecuația pătratică:

.

Raspuns: 0; unu.

5. Ecuații omogene în raport cu funcțiile exponențiale.

O ecuație de formă este o ecuație omogenă de gradul doi în raport cu necunoscutele un xși b x. Astfel de ecuații sunt reduse prin împărțirea preliminară a ambelor părți prin și înlocuirea ulterioară cu ecuații patratice.

Exemplul 23. Rezolvați ecuația.

Rezolvare: Împărțiți ambele părți ale ecuației la:

Punând , obținem o ecuație pătratică cu rădăcini .

Acum problema se reduce la rezolvarea setului de ecuații . Din prima ecuație, aflăm că . A doua ecuație nu are rădăcini, deoarece pentru orice valoare X.

Raspuns: -1/2.

6. Ecuații raționale în raport cu funcțiile exponențiale.

Exemplul 24. Rezolvați ecuația.

Rezolvare: Împărțiți numărătorul și numitorul fracției la 3 xși în loc de două obținem o funcție exponențială:

7. Ecuații de formă .

Astfel de ecuații cu un set de valori admisibile (ODV) determinate de condiția , luând logaritmul ambelor părți ale ecuației, se reduc la echivalent cu ecuația, care la rândul lor sunt echivalente cu mulțimea a două ecuații sau .

Exemplul 25. Rezolvați ecuația:.

.

material didactic.

Rezolvați ecuațiile:

1. ; 2. ; 3. ;

4. ; 5. ; 6. ;

9. ; 10. ; 11. ;

14. ; 15. ;

16. ; 17. ;

18. ; 19. ;

20. ; 21. ;

22. ; 23. ;

24. ; 25. .

26. Aflați produsul rădăcinilor ecuației .

27. Aflați suma rădăcinilor ecuației .

Aflați valoarea expresiei:

28. , unde x0- rădăcina ecuaţiei;

29. , unde x0 este rădăcina ecuației .

Rezolvați ecuația:

31. ; 32. .

Raspunsuri: zece; 2.-2/9; 3. 1/36; 4,0, 0,5; cincizeci; 6,0; 7.-2; 8,2; 9,1, 3; 10,8; 11,5; 12,1; 13. ¼; 14,2; 15. -2, -1; 16.-2, 1; 17,0; 18,1; 19,0; 20,-1, 0; 21.-2, 2; 22.-2, 2; 23,4; 24.-1, 2; 25. -2, -1, 3; 26. -0,3; 27,3; 28,11; 29,54; 30. -1, 0, 2, 3; 31.; 32. .

Subiectul numărul 8.

inegalități exponențiale.

1º. Se numește o inegalitate care conține o variabilă în exponent inegalitate exemplară.

2º. Decizie inegalități exponențiale tipul se bazează pe următoarele afirmații:

dacă , atunci inegalitatea este echivalentă cu ;

dacă , atunci inegalitatea este echivalentă cu .

La rezolvarea inegalităților exponențiale se folosesc aceleași tehnici ca și la rezolvarea ecuațiilor exponențiale.

Exemplul 26. Rezolvați inegalitatea (metoda de trecere la o singură bază).

Soluție: Pentru că , atunci inegalitatea dată poate fi scrisă ca: . Deoarece , această inegalitate este echivalentă cu inegalitatea .

Rezolvând ultima inegalitate, obținem .

Exemplul 27. Rezolvați inegalitatea: ( metoda de a scoate factorul comun din paranteze).

Rezolvare: Scoatem parantezele din partea stângă a inegalității, din partea dreaptă a inegalității și împărțim ambele părți ale inegalității la (-2), schimbând semnul inegalității la opus:

Din moment ce , atunci în trecerea la inegalitatea indicatorilor, semnul inegalității se schimbă din nou la opus. Primim . Astfel, mulțimea tuturor soluțiilor acestei inegalități este intervalul .

Exemplul 28. Rezolvați inegalitatea ( metoda de introducere a unei noi variabile).

Soluție: Să . Atunci această inegalitate ia forma: sau , a cărui soluție este intervalul .

De aici. Deoarece funcția este în creștere, atunci .

material didactic.

Precizați setul de soluții ale inegalității:

1. ; 2. ; 3. ;

6. La ce valori X punctele graficului funcției se află sub linie?

7. La ce valori X punctele graficului funcției nu se află sub linie?

Rezolvați inegalitatea:

8. ; 9. ; 10. ;

13. Indicați cea mai mare soluție întreagă a inegalității .

14. Aflați produsul dintre soluțiile celui mai mare întreg și cel mai mic întreg al inegalității .

Rezolvați inegalitatea:

15. ; 16. ; 17. ;

18. ; 19. ; 20. ;

21. ; 22. ; 23. ;

24. ; 25. ; 26. .

Găsiți domeniul de aplicare al funcției:

27. ; 28. .

29. Găsiți setul de valori ale argumentelor pentru care valorile fiecăreia dintre funcții sunt mai mari decât 3:

și .

Raspunsuri: 11,3; 12,3; 13.-3; 14,1; 15. (0; 0,5); șaisprezece.; 17. (-1; 0)U(3; 4); 18. [-2; 2]; 19. (0; +∞); 20.(0; 1); 21. (3; +∞); 22. (-∞; 0)U(0,5; +∞); 23.(0; 1); 24. (-1; 1); 25. (0; 2]; 26. (3; 3,5)U (4; +∞); 27. (-∞; 3)U(5); 28. )