General theorems of dynamics, technical mechanics. General theorems of dynamics. Dynamics of a material system and a rigid body

home

Differential equations of system motion.

We apply the second (fundamental) law of dynamics, we get We obtain a similar type of equation for any point in the system, i.e. in total for the system under consideration there will be n such equations (k= 1, 2….n). This system of equations is

differential equations of motion of a mechanical system in vector form.

Projecting equalities (2) onto some coordinate axes, we obtain a system of differential equations of motion of the system in projections onto these axes.

As a result of integrating a system of differential equations (which is very difficult), we obtain the laws of motion of each point of the system. It is much more convenient to determine some summary characteristics of the movement of the entire system as a whole, and from them, if required, to find the corresponding parameters of the movement of individual points of the system.

Such characteristics are measures of the motion of the system: momentum, angular momentum, kinetic energy.

Moreover, each of these measures for a system is defined as the sum of the corresponding measures of motion of all its points.

Accordingly, the impacts on the system are considered in total (the main vector and the main moment of forces applied to the system, the amount of work, etc.). The relationship between the measures of movement of the system and the measures of influence on it is expressed by general theorems

systems of material points.

General theorems of system dynamics are consequences of the system of equations (2).

2) System mass. Center of mass

A mechanical system is a system of material points, each of which has a certain mass and occupies a certain position in space at a given moment in time.

For the convenience of solving problems of dynamics of mechanical systems, it is desirable to have some generalized (i.e., total) characteristics that would reflect both the mass of the system and its “mass geometry,” i.e. location in space of material points of the system.

The mass of the system M is equal to the arithmetic sum of the masses of all points or bodies forming the system:

The center of mass of a mechanical system is the geometric point C, the radius of which is the vector

where radius is the vector of points forming the system.

Masses of points of a mechanical system

The center of mass of the system is not a material point, but a geometric one. It may not coincide with any material point of the system. The center of mass of a system characterizes the distribution of masses in the system.

Theorem on the motion of the center of mass of a mechanical system.

Theorem: The center of mass of the system moves as a material point, the mass of which is equal to the mass of the entire system and to which all external forces acting on the system are applied.

Where is the acceleration of the center of mass.

The main vector of external forces.

Projecting both sides of the equation onto the coordinate axes, we get:

where ,, are the coordinates of the center of mass.

From the theorem on the motion of the center of mass, the following important corollaries can be obtained, which express law of conservation of the center of mass of a mechanical system.

If the geometric system of all external forces acting on the system is equal to 0 (), then this means that or, i.e. the center of mass of this system moves with a speed constant in magnitude and direction (in other words, uniformly and rectilinearly). In a particular case, if at first the center of mass was at rest () then it will remain at rest i.e. ().

If the external forces acting on the system are such that the sum of their projections onto some axis (for example, the X axis is equal to 0, that is, the projection of the velocity of the center of mass of the system onto this axis is a constant value. In the particular case, if at the initial moment, then at any subsequent moment in time this value will remain the same, and therefore the coordinate of the center of mass of the system will not change, i.e. = const.

Theorems on the change in momentum of a point and a system

Definition: the amount of motion of a material point is a vector quantity equal to the product of the point’s mass and its velocity vector. A vector is applied to a moving point.

Definition: The amount of motion of a mechanical system is a vector equal to the geometric sum of the amounts of motion of all points of the system.

The vector is a free vector. As a rule, the velocities of all points of the system are different and therefore direct summation of vectors on the right side of the equality is difficult.

Let's use the formula to determine the center of mass of a mechanical system (1)

Or we can write it in the form

Differentiating both parts of the expression with respect to time we obtain:

Comparing formulas (4) and (5), we find that the amount of motion of the system is equal to the product of the mass of the entire system and the speed of its center of mass.

A vector is a generalized vector characteristic of the motion of the entire mechanical system. In general, the motion of a system, its momentum can be considered as a characteristic of the translational part of the motion of the system together with the center of mass. If, when the system (body) moves, the center of mass is stationary, then the amount of motion will be equal to 0. For example, the amount of motion of a body rotating around a fixed axis passing through its center of mass.

Let us write down the second law of dynamics for a material point: taking into account that we obtain (7)

At each moment of time, the time derivative of the momentum of a point is equal to the force acting on the point.

If both sides of equality (7) are multiplied by dt, then we get the vector quantity on the right side of this equality that characterizes the action exerted on the body by the force in an elementary period of time dt this quantity is called the elementary impulse of force, i.e.

Theorem on the motion of the center of mass. Differential equations of motion of a mechanical system. Theorem on the motion of the center of mass of a mechanical system. Law of conservation of motion of the center of mass.

Theorem on the change in momentum. The amount of motion of a material point. Elementary impulse of force. An impulse of force over a finite period of time. Theorem on the change in momentum of a point in differential and finite forms.

The amount of motion of a mechanical system; its expression through the mass of the system and the speed of its center of mass. The theorem on the change in momentum of a mechanical system in differential and finite forms. Law of conservation of momentum of a mechanical system.

Theorem on the change in angular momentum. The moment of momentum of a material point relative to the center and relative to the axis. Theorem on the change in angular momentum of a point.

The principal moment of momentum or kinetic moment of a mechanical system relative to the center and relative to the axis. The kinetic moment of a rotating rigid body about the axis of rotation. Theorem on the change in the kinetic moment of a mechanical system. Law of conservation of angular momentum of a mechanical system.

Theorem on the change in kinetic energy. Kinetic energy of a material point. Elementary work of force; analytical expression of elementary work. The work done by a force on the final displacement of the point of its application. The work of gravity, elastic force and gravitational force. Power. Theorem on the change in kinetic energy of a point.

Kinetic energy of a mechanical system. Kinetic energy of a rigid body during translational motion, during rotation around a fixed axis and during plane-parallel motion of the body. Theorem on the change in kinetic energy of a mechanical system. The sum of the work done by internal forces in a solid body is equal to zero. Work and power of forces applied to a rigid body rotating around a fixed axis.

D'Alembert's principle. The principle of possible movements. The inertial force of a material point. D'Alembert's principle for a material point and a mechanical system.

Lecture 3. General theorems of dynamics

Dynamics of a system of material points is an important branch of theoretical mechanics. Here we mainly consider problems about the motion of mechanical systems (systems of material points) with a finite number of degrees of freedom - the maximum number of independent parameters that determine the position of the system. The main task of system dynamics is the study of the laws of motion of a rigid body and mechanical systems.

The simplest approach to studying the motion of a system, consisting of N material points, comes down to considering the movements of each individual point of the system. In this case, all forces acting on each point of the system, including the forces of interaction between points, must be determined.

Determining the acceleration of each point in accordance with Newton’s second law (1.2), we obtain for each point three scalar differential laws of motion of the second order, i.e. 3 N differential laws of motion for the entire system.

To find the equations of motion of a mechanical system based on given forces and initial conditions for each point of the system, the resulting differential laws must be integrated. This problem is difficult even in the case of two material points that move only under the influence of interaction forces according to the law of universal attraction (two-body problem), and extremely difficult in the case of three interacting points (three-body problem).

Therefore, it is necessary to find methods for solving problems that would lead to solvable equations and give an idea of ​​​​the movement of a mechanical system. General theorems of dynamics, being a consequence of the differential laws of motion, allow us to avoid the complexity that arises during integration and obtain the necessary results.

3. 1. General notes

We will number the points of the mechanical system with indices i, j, k etc., which run through all the values 1, 2, 3… N, Where N – number of points of the system. Physical quantities related to k th point are designated by the same index as the point. For example, express the radius vector and speed, respectively k th point.

Each point of the system is acted upon by forces of two origins: firstly, forces whose sources lie outside the system, called external forces and designated ; secondly, forces from other points of a given system, called internal forces and designated . Internal forces satisfy Newton's third law. Let us consider the simplest properties of internal forces acting on the entire mechanical system in any state.

First property. The geometric sum of all internal forces of the system (the main vector of internal forces) is equal to zero.

Indeed, if we consider any two arbitrary points of the system, for example and (Fig. 3.1), then for them , because action and reaction forces are always equal in magnitude, acting along one line of action in the opposite direction, which connects the interacting points. The main vector of internal forces consists of pairs of forces of interacting points, therefore

(3.1)

Second property. The geometric sum of the moments of all internal forces relative to an arbitrary point in space is equal to zero.

Let us consider a system of moments of forces and relative to the point ABOUT(Fig. 3.1). From (Fig. 3.1). it's clear that

,

because both forces have the same arms and opposite directions of vector moments. Principal moment of internal forces relative to a point ABOUT consists of the vector sum of such expressions and is equal to zero. Hence,

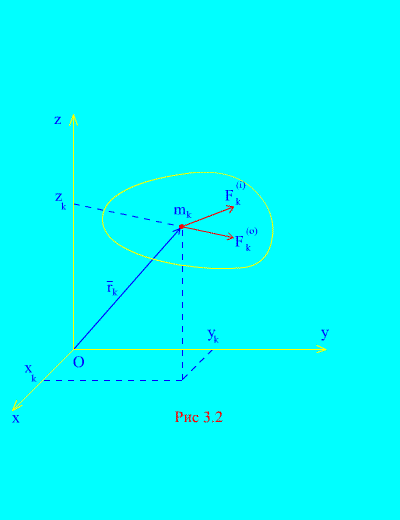
Let external and internal forces acting on a mechanical system consisting of N points (Fig. 3.2). If the resultant of external forces and the resultant of all internal forces are applied to each point of the system, then for any k th point of the system, differential equations of motion can be drawn up. There will be a total of such equations N:

and in projections onto fixed coordinate axes 3 N:

(3.4)

Vector equations (3.3) or equivalent scalar equations (3.4) represent the differential laws of motion of material points of the entire system. If all points move parallel to one plane or one straight line, then the number of equations (3.4) in the first case will be 2 N, in the second N.

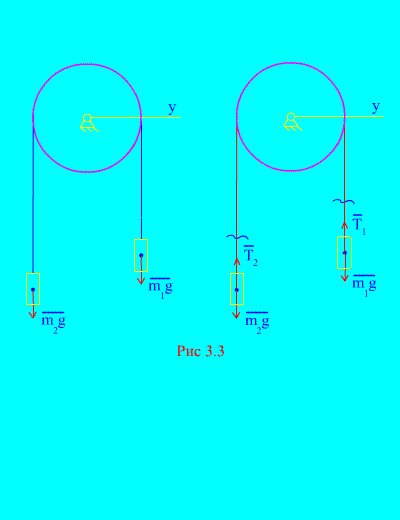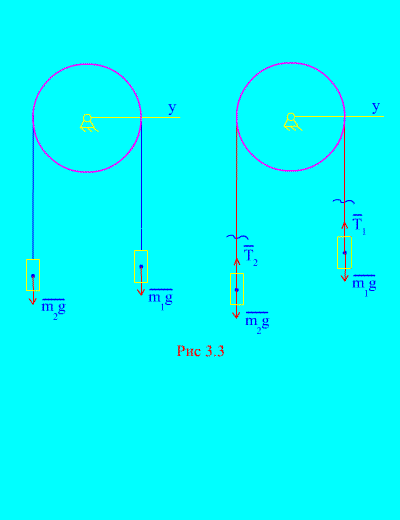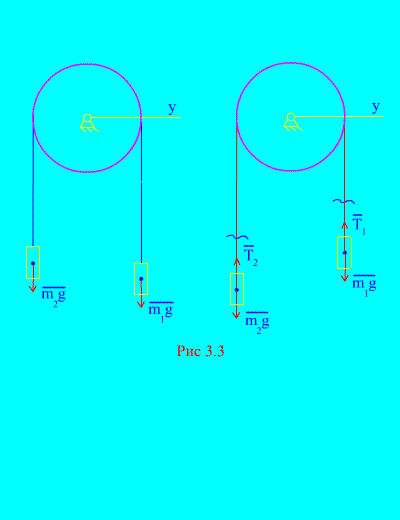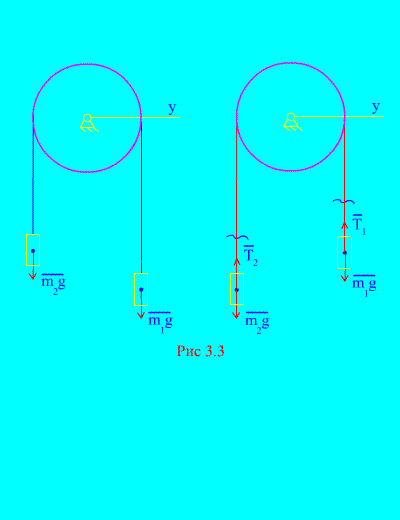
Example 1. Two masses are connected to each other by an inextensible cable thrown over a block (Fig. 3.3). Neglecting friction forces, as well as the mass of the block and cable, determine the law of movement of loads and cable tension.

Solution. The system consists of two material bodies (connected by an inextensible cable) moving parallel to the same axis X. Let us write down the differential laws of motion in projections onto the axis X for every body.

Let the right weight fall with acceleration, then the left weight will rise with acceleration. We mentally free ourselves from the connection (cable) and replace it with reactions and (Fig. 3.3). Considering the bodies to be free, let us draw up the differential laws of motion in projection onto the axis X(meaning that the thread tensions are internal forces, and the weight of the loads are external):

Since and (the bodies are connected by an inextensible cable), we obtain

Solving these equations for acceleration and cable tension T, we get

.

Note that the tension in the cable is not equal to the force of gravity of the corresponding load.

3. 2. Theorem on the motion of the center of mass

It is known that a rigid body and a mechanical system in a plane can move quite complexly. The first theorem on the motion of a body and a mechanical system can be arrived at as follows: throw a k.-l. an object consisting of many solid bodies fastened together. It is clear that he will fly in a parabola. This was revealed when studying the movement of the point. However, now the object is not a point. It turns and sways during its flight around some effective center that moves in a parabola. The first theorem about the movement of complex objects says that a certain effective center is the center of mass of a moving object. The center of mass is not necessarily located in the body itself; it can lie somewhere outside it.

Theorem. The center of mass of a mechanical system moves as a material point with a mass equal to the mass of the entire system, to which all external forces acting on the system are applied.

To prove the theorem, we rewrite the differential laws of motion (3.3) in the following form:

(3.5)

Where N – number of points of the system.

Let’s add the equations together term by term:

(A)

The position of the center of mass of the mechanical system relative to the selected coordinate system is determined by formula (2.1): Where M– mass of the system. Then the left side of equality (a) will be written

The first sum on the right side of equality (a) is equal to the main vector of external forces, and the last, by the property of internal forces, is equal to zero. Then equality (a), taking into account (b), will be rewritten

, (3.6)

those. the product of the mass of the system and the acceleration of the center of its mass is equal to the geometric sum of all external forces acting on the system.

From equation (3.6) it follows that internal forces do not directly affect the movement of the center of mass. However, in some cases they are the cause of the appearance of external forces applied to the system. Thus, the internal forces driving the driving wheels of a car into rotation cause an external adhesion force applied to the wheel rim to act on it.

Example 2. The mechanism, located in a vertical plane, is installed on a horizontal smooth plane and attached to it with bars rigidly fixed to the surface TO And L (Fig. 3.4).

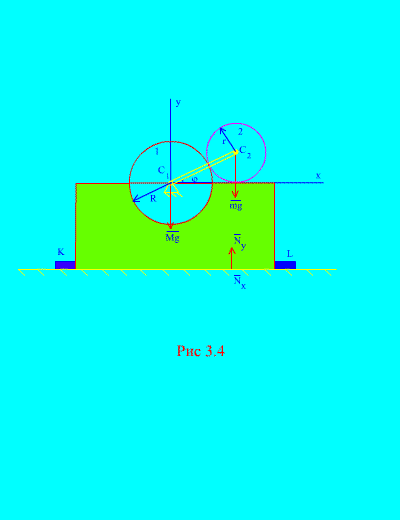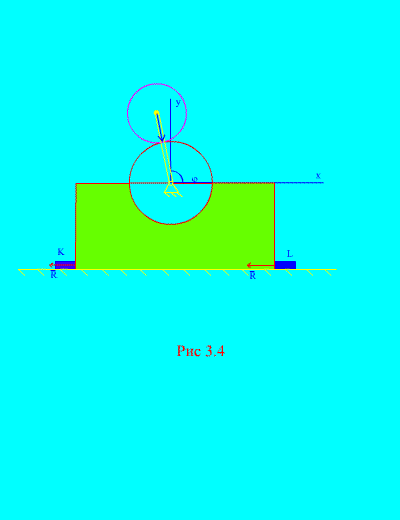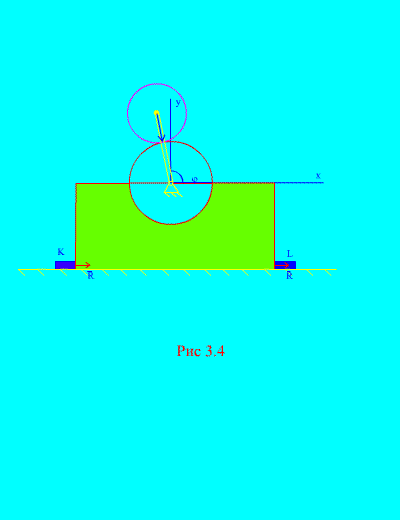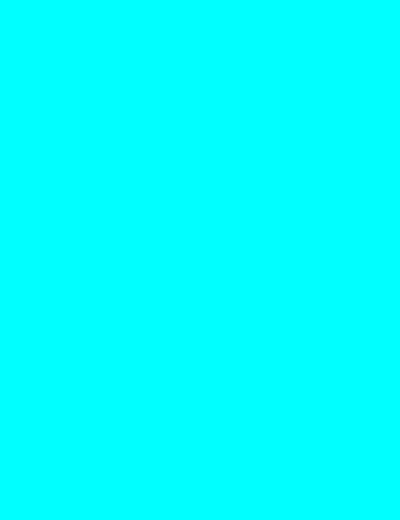
Disc 1 radius R motionless. Disk 2 mass m and radius r attached to a crank, length R+ r at the point C 2. The crank rotates at a constant

angular speed. At the initial moment, the crank occupied the right horizontal position. Neglecting the mass of the crank, determine the maximum horizontal and vertical forces acting on the bars if the total mass of the frame and wheel 1 is equal to M. Also consider the behavior of the mechanism in the absence of bars.

Solution. The system consists of two masses ( N=2 ): fixed disk 1 with a frame and movable disk 2. Direct the axis at through the center of gravity of the stationary disk vertically upward, axis X– along the horizontal plane.

Let us write the theorem on the motion of the center of mass (3.6) in coordinate form

The external forces of this system are: the weight of the frame and the fixed disk - Mg, moving disk weight – mg, - the total horizontal reaction of the bolts, - the normal total reaction of the plane. Hence,

Then the laws of motion (b) will be rewritten

Let's calculate the coordinates of the center of mass of the mechanical system:

; (G)

as can be seen from (Fig. 3.4), , , (crank angle), . Substituting these expressions into (d) and calculating the second derivatives with respect to time t from , , we get that

(e)

Substituting (c) and (e) into (b), we find

The horizontal pressure acting on the bars is greatest and least when cos = 1 accordingly, i.e.

The pressure of the mechanism on the horizontal plane has the highest and lowest values ​​when sin accordingly, i.e.

In fact, the first problem of dynamics has been solved: according to the known equations of motion of the center of mass of the system (d), the forces involved in the movement are restored.

In the absence of bars K And L (Fig. 3.4), the mechanism may begin to bounce above the horizontal plane. This will take place when, i.e. when , it follows that the angular velocity of rotation of the crank, at which the mechanism bounces, must satisfy the equality

.

3. 3. Law of conservation of motion of the center of mass

If the main vector of external forces acting on the system is equal to zero, i.e. , then from(3.6)it follows that the acceleration of the center of mass is zero, therefore, the speed of the center of mass is constant in magnitude and direction. If, in particular, at the initial moment the center of mass is at rest, then it is at rest for the entire time while the main vector of external forces is equal to zero.

Several corollaries follow from this theorem.

· Internal forces alone cannot change the nature of the movement of the system's center of mass.

· If the main vector of external forces acting on the system is zero, then the center of mass is at rest or moves uniformly and rectilinearly.

· If the projection of the main vector of the external forces of the system onto some fixed axis is equal to zero, then the projection of the velocity of the center of mass of the system onto this axis does not change.

· A pair of forces applied to a rigid body cannot change the movement of its center of mass (it can only cause the body to rotate around the center of mass).

Let's consider an example illustrating the law of conservation of motion of the center of mass.

Example 3. Two masses are connected by an inextensible thread thrown through a block (Fig. 3.5), fixed on a wedge with a mass M. The wedge rests on a smooth horizontal plane. At the initial moment the system was at rest. Find the displacement of the wedge along the plane when the first load is lowered to a height N. Neglect the mass of the block and thread.

Solution. External forces acting on the wedge together with loads are gravity, and Mg, as well as the normal reaction of a smooth horizontal surface N. Consequently,

Since at the initial moment the system was at rest, we have .

Let us calculate the coordinates of the center of mass of the system at and at the moment t 1 when the load weighs g will descend to a height H.

For the moment:

,

Where , , X– respectively, the coordinates of the center of mass of loads weighing g, g and a wedge weighing Mg.

Let us assume that the wedge at the moment of time moves in the positive direction of the axis Ox by the amount L, if the weight of the load drops to a height N. Then, for the moment

because the loads together with the wedge will move to L to the right, and the load will move upward along the wedge. Since , then after calculations we get

.

3.4. System movement quantity

3.4.1. Calculation of system momentum

The momentum of a material point is a vector quantity equal to the product of the mass of the point and its velocity vector

Unit of measurement of momentum -

The momentum of a mechanical system is the vector sum of the momentum of individual points of the system, i.e.

Where N – number of points of the system.

The momentum of a mechanical system can be expressed in terms of the mass of the system M and the speed of the center of mass. Really,

those. The momentum of the system is equal to the product of the mass of the entire system and the speed of its center of mass. The direction is the same as the direction (Fig. 3.6)

In projections onto rectangular axes we have

where , , are projections of the velocity of the system’s center of mass.

Here M– mass of the mechanical system; does not change when the system moves.

These results are especially convenient to use when calculating the quantities of motion of rigid bodies.

From formula (3.7) it is clear that if a mechanical system moves in such a way that its center of mass remains stationary, then the momentum of the system remains equal to zero.

3.4.2. Elementary and full force impulse

The action of a force on a material point over time dt can be characterized by an elementary impulse. Total force impulse over time t, or force impulse, determined by the formula

or in projections onto axis coordinates

(3.8a)

The unit of force impulse is .

3.4.3. Theorem on the change in momentum of a system

Let external and internal forces be applied to the points of the system. Then for each point of the system we can apply the differential laws of motion (3.3), keeping in mind that :

.

Summing over all points of the system, we obtain

By the property of internal forces and by definition we have

(3.9)

Multiplying both sides of this equation by dt, we obtain a theorem on the change in momentum in differential form:

, (3.10)

those. the differential momentum of a mechanical system is equal to the vector sum of the elementary impulses of all external forces acting on points of the mechanical system.

Calculating the integral of both sides (3.10) over time from 0 to t, we obtain the theorem in finite or integral form

(3.11)

In projections onto the coordinate axes we will have

Change in momentum of a mechanical system over timet, is equal to the vector sum of all impulses of external forces acting on points of the mechanical system during the same time.

Example 4. Load weight m descends down an inclined plane from rest under the influence of a force F, proportional to time: , where (Fig. 3.7). What speed will the body acquire after t seconds after the start of movement, if the coefficient of sliding friction of the load on the inclined plane is equal to f.

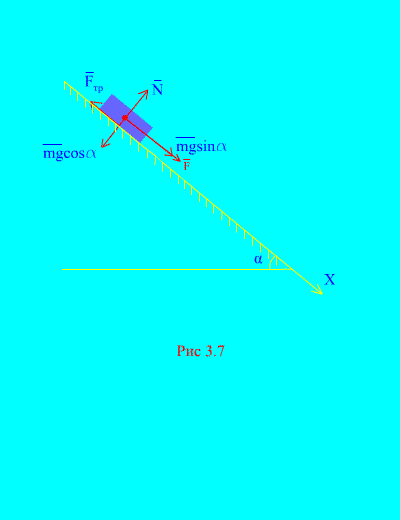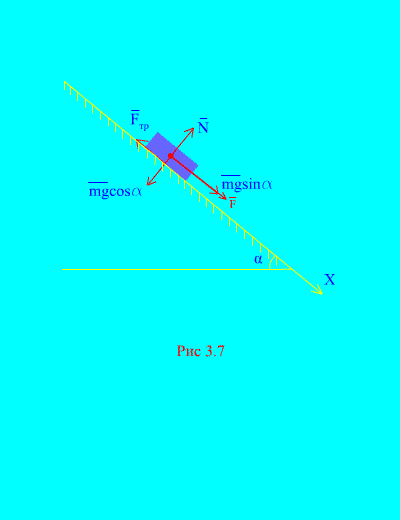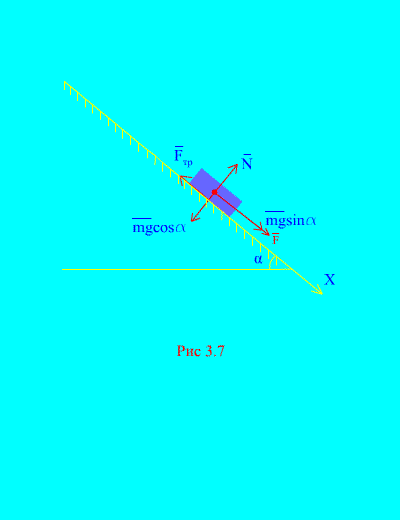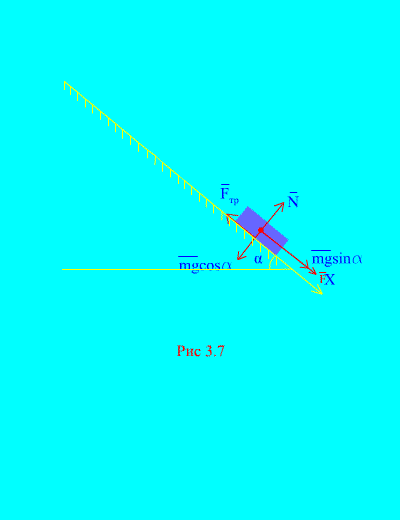
Solution. Let us depict the forces applied to the load: mg – load gravity force, N is the normal reaction of the plane, is the sliding friction force of the load on the plane, and . The direction of all forces is shown in (Fig. 3.7).

Let's direct the axis X along the inclined plane downwards. Let us write the theorem about the change in momentum (3.11) in projection onto the axis X:

(A)

According to the condition, because at the initial moment of time the load was at rest. The sum of the projections of the impulses of all forces onto the x axis is equal to

Hence,

,

.

3.4.4. Laws of conservation of momentum

Conservation laws are obtained as special cases of the theorem on the change in momentum. Two special cases are possible.

· If the vector sum of all external forces applied to the system is equal to zero, i.e. , then from the theorem it follows (3.9) , What ,

those. if the main vector of the external forces of the system is zero, then the amount of motion of the system is constant in magnitude and direction.

· If the projection of the main vector of external forces onto any coordinate axis is equal to zero, for example Ox, i.e. , then the projection of the momentum onto this axis is a constant value.

Let's consider an example of applying the law of conservation of momentum.

Example 5. A ballistic pendulum is a body with a mass suspended on a long thread (Fig. 3.8).

A bullet of mass , moving with speed V and hitting a stationary body, gets stuck in it, and the body deviates. What was the speed of the bullet if the body rose to a height h ?

Solution. Let the body with the stuck bullet acquire speed. Then, using the law of conservation of momentum during the interaction of two bodies, we can write .

Speed ​​can be calculated using the law of conservation of mechanical energy . Then . As a result we find

.

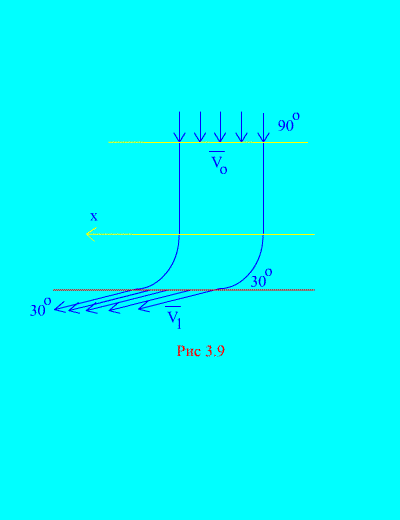
Example 6. Water enters a stationary channel (Fig. 3.9) variable cross-section with speed at an angle to the horizontal; cross-sectional area of ​​the channel at the entrance; the speed of water at the exit from the channel makes an angle with the horizon.

Determine the horizontal component of the reaction that water has on the channel walls. Density of water .

Solution. We will determine the horizontal component of the reaction exerted by the channel walls on water. This force is equal in magnitude and opposite in sign to the desired force. We have, according to (3.11a),

. (A)

We calculate the mass of the volume of liquid entering the channel during time t:

The quantity rAV 0 is called second mass - the mass of liquid flowing through any section of the pipe per unit time.

The same amount of water leaves the canal during the same time. The initial and final speeds are given in the condition.

Let us calculate the right side of equality (a), which determines the sum of projections onto the horizontal axis of external forces applied to the system (water). The only horizontal force is the horizontal component of the resultant wall reaction Rx. This force is constant during steady water movement. That's why

. (V)

Substituting (b) and (c) into (a), we get

3.5. Kinetic moment of the system

3.5.1. Main moment of momentum of the system

Let be the radius vector of a point with the mass of the system relative to some point A, called the center (Fig. 3.10).

Momentum of momentum (kinetic moment) of a point relative to center A called a vector , determined by the formula

. (3.12)

In this case, the vector directed perpendicular to the plane passing through the center A and vector .

Momentum of momentum (kinetic moment) of a point relative to the axis is called the projection onto this axis of the moment of momentum of a point relative to any center chosen on this axis.

The main moment of momentum (kinetic moment) of the system relative to center A is called the quantity

(3.13)

The main moment of momentum (kinetic moment) of the system relative to the axis is called the projection onto this axis of the main moment of momentum of the system relative to any chosen on this center axis.

3.5.2. Kinetic moment of a rotating rigid body about the axis of rotation

Let's align the fixed point ABOUT body lying on the axis of rotation ABOUTz, with the origin of the coordinate system Ohooz, the axes of which will rotate with the body (Fig. 3.11). Let be the radius vector of a point of the body relative to the origin of coordinates; its projection on the axis will be denoted by , , . We denote the projections of the angular velocity vector of the body on the same axes as 0, 0, ().

MOMENTUM THEOREM (in differential form).

1. For a point: the derivative of the momentum of the point with respect to time is equal to the resultant of the forces applied to the point:

or in coordinate form:

2. For a system: the derivative of the momentum of the system with respect to time is equal to the main vector of external forces of the system (vector sum of external forces applied to the system):

or in coordinate form:

MOMENTUM THEOREM (momentum theorem in final form).

1. For a point: the change in the momentum of the point over a finite period of time is equal to the sum of the impulses applied to the force point (or the resultant impulse of the forces applied to the point)

or in coordinate form:

2. For a system: the change in the momentum of the system over a finite period of time is equal to the sum of the impulses of external forces:

or in coordinate form:

Consequences: in the absence of external forces, the amount of motion of the system is a constant value; if the external forces of the system are perpendicular to a certain axis, then the projection of the momentum onto this axis is a constant value.

MOMENTUM THEOREM

1. For a point: The time derivative of the moment of momentum of the point relative to some center (axis) is equal to the sum of the moments of forces applied to the point relative to the same center (axis):

2. For the system:

The time derivative of the moment of momentum of the system relative to some center (axis) is equal to the sum of the moments of the external forces of the system relative to the same center (axis):

Consequences: if the external forces of the system do not provide a moment relative to a given center (axis), then the angular momentum of the system relative to this center (axis) is a constant value.

If the forces applied to a point do not produce a moment relative to a given center, then the angular momentum of the point relative to this center is a constant value and the point describes a flat trajectory.

KINETIC ENERGY THEOREM

1. For a point: the change in the kinetic energy of a point at its final displacement is equal to the work of the active forces applied to it (the tangential components of the reactions of non-ideal bonds are included in the number of active forces):

For the case of relative motion: the change in the kinetic energy of a point during relative motion is equal to the work of the active forces applied to it and the transfer force of inertia (see "Special cases of integration"):

2. For a system: the change in the kinetic energy of the system at a certain displacement of its points is equal to the work of the external active forces applied to it and the internal forces applied to the points of the system, the distance between which changes:

If the system is immutable (solid body), then ΣA i =0 and the change in kinetic energy is equal to the work of only external active forces.

THEOREM ABOUT THE MOTION OF THE CENTER OF MASS OF A MECHANICAL SYSTEM. The center of mass of a mechanical system moves as a point whose mass is equal to the mass of the entire system M=Σm i , to which all external forces of the system are applied:

or in coordinate form:

where is the acceleration of the center of mass and its projection on the Cartesian coordinate axes; external force and its projections on the Cartesian coordinate axes.

MOMENTUM THEOREM FOR THE SYSTEM, EXPRESSED IN THROUGH THE MOTION OF THE CENTER OF MASS.

The change in the speed of the center of mass of the system over a finite period of time is equal to the impulse of the external forces of the system over the same period of time, divided by the mass of the entire system.

Theorem on the motion of the center of mass. Differential equations of motion of a mechanical system. Theorem on the motion of the center of mass of a mechanical system. Law of conservation of motion of the center of mass.

Theorem on the change in momentum. The amount of motion of a material point. Elementary impulse of force. Force impulse for a finite period of time and its projection onto the coordinate axes. Theorem on the change in momentum of a material point in differential and finite forms.

The amount of motion of a mechanical system; its expression through the mass of the system and the speed of its center of mass. Theorem on the change in momentum of a mechanical system in differential and finite forms. Law of conservation of momentum of mechanical

(The concept of a body and a point of variable mass. Meshchersky’s equation. Tsiolkovsky’s formula.)

Theorem on the change in angular momentum. The moment of momentum of a material point relative to the center and relative to the axis. Theorem on the change in angular momentum of a material point. Central power. Conservation of angular momentum of a material point in the case of a central force. (The concept of sector velocity. The law of areas.)

The principal moment of momentum or kinetic moment of a mechanical system relative to the center and relative to the axis. The kinetic moment of a rotating rigid body about the axis of rotation. Theorem on the change in the kinetic moment of a mechanical system. Law of conservation of angular momentum of a mechanical system. (The theorem on the change in the angular momentum of a mechanical system in relative motion with respect to the center of mass.)

Theorem on the change in kinetic energy. Kinetic energy of a material point. Elementary work of force; analytical expression of elementary work. The work done by a force on the final displacement of the point of its application. The work of gravity, elastic force and gravitational force. Theorem on the change in the kinetic energy of a material point in differential and finite forms.

Kinetic energy of a mechanical system. Formulas for calculating the kinetic energy of a rigid body during translational motion, during rotation around a fixed axis and in the general case of motion (in particular, during plane-parallel motion). Theorem on the change in kinetic energy of a mechanical system in differential and finite forms. The sum of the work done by internal forces in a solid body is equal to zero. Work and power of forces applied to a rigid body rotating around a fixed axis.

The concept of a force field. Potential force field and force function. Expression of force projections through the force function. Surfaces of equal potential. The work of a force on the final displacement of a point in a potential force field. Potential energy. Examples of potential force fields: uniform gravitational field and gravitational field. Law of conservation of mechanical energy.

Rigid body dynamics. Differential equations of translational motion of a rigid body. Differential equation for the rotation of a rigid body around a fixed axis. Physical pendulum. Differential equations of plane motion of a rigid body.

D'Alembert's principle. D'Alembert's principle for a material point; inertial force. D'Alembert's principle for a mechanical system. Bringing the inertia forces of points of a rigid body to the center; main vector and main moment of inertia forces.

(Determination of dynamic reactions of bearings during rotation of a rigid body around a fixed axis. The case when the axis of rotation is the main central axis of inertia of the body.)

The principle of possible movements and the general equation of dynamics. Connections imposed on a mechanical system. Possible (or virtual) movements of a material point and a mechanical system. The number of degrees of freedom of the system. Ideal connections. The principle of possible movements. General equation of dynamics.

Equations of motion of a system in generalized coordinates (Lagrange equations). Generalized coordinates of the system; generalized speeds. Expression of elementary work in generalized coordinates. Generalized forces and their calculation; the case of forces with potential. Conditions for the equilibrium of a system in generalized coordinates. Differential equations of motion of a system in generalized coordinates or Lagrange equations of the 2nd kind. Lagrange equations in the case of potential forces; Lagrange function (kinetic potential).

The concept of equilibrium stability. Small free vibrations of a mechanical system with one degree of freedom near the position of stable equilibrium of the system and their properties.

Elements of impact theory. Impact phenomenon. Impact force and impact impulse. The action of an impact force on a material point. Theorem on the change in momentum of a mechanical system upon impact. Direct central impact of the body on a stationary surface; elastic and inelastic impacts. Impact recovery coefficient and its experimental determination. Direct central impact of two bodies. Carnot's theorem.

BIBLIOGRAPHY

Basic

Butenin N.V., Lunts Ya-L., Merkin D.R. Course of theoretical mechanics. T. 1, 2. M., 1985 and previous editions.

Dobronravov V.V., Nikitin N.N. Course of theoretical mechanics. M., 1983.

Starzhinsky V. M. Theoretical mechanics. M., 1980.

Targ S. M. Short course in theoretical mechanics. M., 1986 and previous editions.

Yablonsky A. A., Nikiforova V. M. Course of theoretical mechanics. Part 1. M., 1984 and previous editions.

Yablonsky A. A. Course of theoretical mechanics. Part 2. M., 1984 and previous editions.

Meshchersky I. V. Collection of problems on theoretical mechanics. M., 1986 and previous editions.

Collection of problems on theoretical mechanics/Ed. K. S. Kolesnikova. M., 1983.

Additional

Bat M. I., Dzhanelidze G. Yu., Kelzon A. S. Theoretical mechanics in examples and problems. Parts 1, 2. M., 1984 and previous editions.

Collection of problems on theoretical mechanics/5razhnichen/so N. A., Kan V. L., Mintzberg B. L. and others. M., 1987.

Novozhilov I. V., Zatsepin M. F. Typical computer-based calculations in theoretical mechanics. M., 1986,

Collection of assignments for coursework in theoretical mechanics / Ed. A. A. Yablonsky. M., 1985 and previous editions (contains examples of problem solving).