How to find the smallest value of a function in terms of the derivative. Largest and smallest value of a function on a segment

Let the function y =f(NS) is continuous on the segment [ a, b]. As you know, such a function on this segment reaches the largest and the smallest values. The function can take these values ​​either at the inner point of the segment [ a, b], or on the border of the segment.

To find the largest and smallest values ​​of the function on the segment [ a, b] necessary:

1) find the critical points of the function in the interval ( a, b);

2) calculate the values ​​of the function at the found critical points;

3) calculate the values ​​of the function at the ends of the segment, that is, for x=a and x = b;

4) choose the largest and the smallest of all the calculated values ​​of the function.

Example. Find Largest and Smallest Function Values

on the segment.

Find critical points:

These points lie inside the line segment; y(1) = ‒ 3; y(2) = ‒ 4; y(0) = ‒ 8; y(3) = 1;

at the point x= 3 and at the point x= 0.

Investigation of the function for convexity and inflection point.

Function y = f (x) called convex up in between (a, b) if its graph lies under the tangent drawn at any point of this interval, and is called convex down (concave) if its graph lies above the tangent line.

The point, upon passing through which the convexity is replaced by concavity, or vice versa, is called inflection point.

Study algorithm for convexity and inflection point:

1. Find the critical points of the second kind, that is, the points at which the second derivative is zero or does not exist.

2. Draw critical points on the number line, dividing it into intervals. Find the sign of the second derivative at each interval; if, then the function is convex upward; if, then the function is convex downward.

3. If, when passing through a critical point of the second kind, changes sign and at this point the second derivative is equal to zero, then this point is the abscissa of the inflection point. Find her ordinate.

Asymptotes of the graph of a function. Investigation of the function for asymptotes.

Definition. The asymptote of the graph of a function is called straight, which has the property that the distance from any point on the graph to this straight line tends to zero with an unlimited distance from the origin of the graph point.

There are three types of asymptotes: vertical, horizontal and inclined.

Definition. The straight line is called vertical asymptote function graphics y = f (x) if at least one of the one-sided limits of the function at this point is equal to infinity, that is

where is the discontinuity point of the function, that is, it does not belong to the domain of definition.

Example.

D ( y) = (‒ ∞; 2) (2; + ∞)

x= 2 - break point.

Definition. Straight y =A called horizontal asymptote function graphics y = f (x) at, if

Example.

Definition. Straight y =kx +b (k≠ 0) is called oblique asymptote function graphics y = f (x) at, where

General scheme for the study of functions and plotting.

Function research algorithmy = f (x) :

1. Find the domain of the function D (y).

2. Find (if possible) the points of intersection of the graph with the coordinate axes (for x= 0 and for y = 0).

3. Investigate for evenness and oddness of the function ( y (‒ x) = y (x) ‒ parity; y(‒ x) = ‒ y (x) ‒ odd).

4. Find the asymptotes of the graph of the function.

5. Find the intervals of monotonicity of the function.

6. Find the extrema of the function.

7. Find the intervals of convexity (concavity) and inflection points of the graph of the function.

8. Based on the research carried out, build a graph of the function.

Example. Examine the function and graph it.

1) D (y) =

x= 4 - break point.

2) When x = 0,

(0; - 5) - intersection point with oy.

At y = 0,

3) y(‒ x)= function general view(neither even nor odd).

4) Investigate for asymptotes.

a) vertical

b) horizontal

c) find oblique asymptotes where

‒ Oblique asymptote equation

5) B this equation it is not required to find the intervals of monotonicity of the function.

6)

These critical points split the entire domain of the function on the interval (˗∞; ˗2), (˗2; 4), (4; 10) and (10; + ∞). It is convenient to present the results obtained in the form of the following table.

Sometimes problems B14 come across "bad" functions for which it is difficult to find a derivative. Previously, this was only on probes, but now these tasks are so common that they can no longer be ignored in preparation for the real exam. In this case, other techniques work, one of which is monotony. Definition A function f (x) is called monotonically increasing on a segment if for any points x 1 and x 2 of this segment the following is true: x 1

Definition. A function f (x) is called monotonically decreasing on a segment if for any points x 1 and x 2 of this segment the following is true: x 1 f (x 2). In other words, for an increasing function, the larger the x, the larger the f (x). For a decreasing function, the opposite is true: the larger x, the smaller f (x).

Examples. The logarithm increases monotonically if the base a> 1, and decreases monotonically if 0 0.f (x) = log a x (a> 0; a 1; x> 0) 1, and decreases monotonically if 0 0.f (x) = log ax (a> 0; a 1; x> 0) "> 1, and decreases monotonically if 0 0. f (x) = log ax (a > 0; a 1; x> 0) "> 1, and monotonically decreases if 0 0. f (x) = log ax (a> 0; a 1; x> 0)" title = "(! LANG: Examples . The logarithm increases monotonically if the base a> 1, and decreases monotonically if 0 0.f (x) = log ax (a> 0; a 1; x> 0)"> title="Examples. The logarithm increases monotonically if the base a> 1, and decreases monotonically if 0 0.f (x) = log a x (a> 0; a 1; x> 0)"> !}

Examples. The exponential function behaves similarly to the logarithm: it grows for a> 1 and decreases for 0 0: 1 and decreases at 0 0: "> 1 and decreases at 0 0:"> 1 and decreases at 0 0: "title =" (! LANG: Examples. The exponential function behaves similarly to the logarithm: increases at a> 1 and decreases at 0 0:"> title="Examples. The exponential function behaves similarly to the logarithm: it grows for a> 1 and decreases for 0 0:"> !}

0) or down (a 0) or down (a 9 Parabola vertex coordinates Most often, the function argument is replaced by a square trinomial of the form Its graph is a standard parabola in which we are interested in branches: Parabola branches can go up (for a> 0) or down (a 0) or the largest (a 0) or down (a 0) or down (a 0) or the largest (a 0) or down (a 0) or down (a title = "(! LANG: Coordinates of the vertex of the parabola) Most often, the function argument is replaced by a square trinomial of the form Its graph is a standard parabola, in which we are interested in branches: The branches of a parabola can go up (for a> 0) or down (a

There is no segment in the problem statement. Therefore, there is no need to compute f (a) and f (b). It remains to consider only the extremum points; But there is only one such point, this is the vertex of the parabola x 0, the coordinates of which are calculated literally orally and without any derivatives.

Thus, the solution of the problem is greatly simplified and comes down to just two steps: Write out the equation of the parabola and find its vertex by the formula: Find the value of the original function at this point: f (x 0). If no additional conditions no, that will be the answer.

0. The vertex of the parabola: x 0 = b / (2a) = 6 / (2 · 1) = 6/2 = 3 "title =" (! LANG: Find the smallest value of the function: Solution: Under the root is quadratic function The graph of this function is a parabola with branches up, since the coefficient a = 1> 0. The vertex of the parabola: x 0 = b / (2a) = 6 / (2 · 1) = 6/2 = 3 "class =" link_thumb "> 18 Find the smallest value of the function: Solution: Under the root is a quadratic function The graph of this function is a parabola with branches up, since the coefficient a = 1> 0. The vertex of the parabola: x 0 = b / (2a) = 6 / (2 1) = 6/2 = 3 0. The vertex of the parabola: x 0 = b / (2a) = 6 / (2 1) = 6/2 = 3 "> 0. The vertex of the parabola: x 0 = b / (2a) = 6 / (2 1) = 6/2 = 3 "> 0. Vertex of the parabola: x 0 = b / (2a) = 6 / (2 · 1) = 6/2 = 3" title = "(! LANG: Find the smallest value of the function: Solution: The quadratic function is under the root. The graph of this function is a parabola with branches up, since the coefficient a = 1> 0. The vertex of the parabola: x 0 = b / (2a) = 6 / (2 · 1) = 6/2 = 3"> title="Find the smallest value of the function: Solution: Under the root is a quadratic function The graph of this function is a parabola with branches up, since the coefficient a = 1> 0. The vertex of the parabola: x 0 = b / (2a) = 6 / (2 1) = 6/2 = 3"> !}

Find the smallest value of the function: Solution Under the logarithm, the quadratic function is again. a = 1> 0. The vertex of the parabola: x 0 = b / (2a) = 2 / (2 1) = 2/2 = 1 0. The vertex of the parabola: x 0 = b / (2a) = 2 / (2 1) = 2/2 = 1 "> 0. The vertex of the parabola: x 0 = b / (2a) = 2 / (2 1) = 2/2 = 1 "> 0. Vertex of the parabola: x 0 = b / (2a) = 2 / (2 1) = 2/2 = 1" title = "(! LANG: Find the smallest value of the function: Solution Under The logarithm is again a quadratic function. Graph the parabola with branches up, since a = 1> 0. The vertex of the parabola: x 0 = b / (2a) = 2 / (2 1) = 2/2 = 1"> title="Find the smallest value of the function: Solution Under the logarithm, the quadratic function is again. a = 1> 0. The vertex of the parabola: x 0 = b / (2a) = 2 / (2 1) = 2/2 = 1"> !}

Find the largest value of the function: Solution: The exponent contains a quadratic function Let's rewrite it in its normal form: Obviously, the graph of this function is a parabola, branches down (a = 1

Consequences from the domain of a function Sometimes, to solve Problem B14, it is not enough just to find the vertex of a parabola. The sought value may lie at the end of the segment, and not at all at the extremum point. If the problem does not specify a segment at all, we look at the range of admissible values ​​of the original function. Namely:

0 2. Arithmetic Square root exists only of non-negative numbers: 3. The denominator of the fraction must not be zero: "title =" (! LANG: 1. The argument of the logarithm must be positive: y = log af (x) f (x)> 0 2. The arithmetic square root exists only of non-negative numbers: 3. The denominator of the fraction must not be zero:" class="link_thumb"> 26 !} 1. The argument of the logarithm must be positive: y = log a f (x) f (x)> 0 2. The arithmetic square root exists only of non-negative numbers: 3. The denominator of the fraction must not be zero: 0 2. The arithmetic square root exists only from non-negative numbers: 3. The denominator of a fraction must not be zero: "> 0 2. The arithmetic square root exists only from non-negative numbers: 3. The denominator of a fraction must not equal zero:"> 0 2. Arithmetic square root exists only of non-negative numbers: 3. The denominator of the fraction must not be zero: "title =" (! LANG: 1. The argument of the logarithm must be positive: y = log af (x) f (x)> 0 2. Arithmetic square the root exists only of non-negative numbers: 3. The denominator of the fraction must not be zero:"> title="1. The argument of the logarithm must be positive: y = log a f (x) f (x)> 0 2. The arithmetic square root exists only of non-negative numbers: 3. The denominator of the fraction must not be zero:"> !}

Solution Under the root is again a quadratic function. Its graph is parabola, but the branches are directed downward, since a = 1
Now we find the vertex of the parabola: x 0 = b / (2a) = (2) / (2 Now we calculate the value of the function at the point x 0, as well as at the ends of the ODZ: y (3) = y (1) = 0 So, we got the numbers 2 and 0. We are asked to find the largest number 2. Answer: 2

Please note: the inequality is strict, so the ends do not belong to the ODZ. This is how the logarithm differs from the root, where the ends of the segment are quite suitable for us. We are looking for the vertex of the parabola: x 0 = b / (2a) = 6 / (2 But since we are not interested in the ends of the segment, we consider the value of the function only at the point x 0:

Y min = y (3) = log 0.5 (6) = = log 0.5 (18 9 5) = log 0.5 4 = 2 Answer: -2

How to find the largest and smallest values ​​of a function on a segment?

For this we follow the well-known algorithm:

1 ... We find the ODZ function.

2 ... Find the derivative of the function

3 ... Equating the derivative to zero

4 ... We find the intervals at which the derivative retains its sign, and from them we determine the intervals of increase and decrease of the function:

If on the interval I the derivative of the function 0 "title =" (! LANG: f ^ (prime) (x)> 0">, то функция !} increases in this interval.

If the derivative of the function on the interval I, then the function decreases in this interval.

5 ... We find maximum and minimum points of the function.

V the maximum point of the function, the derivative changes sign from "+" to "-".

V the minimum point of the functionthe derivative changes sign from "-" to "+".

6 ... Find the value of the function at the ends of the segment,

• then we compare the value of the function at the ends of the segment and at the maximum points, and choose the largest of them, if we need to find the largest value of the function
• or we compare the value of the function at the ends of the segment and at the minimum points, and choose the smallest of them if we need to find the smallest value of the function

However, depending on how the function behaves on the segment, this algorithm can be significantly reduced.

Consider the function ... The graph of this function looks like this:

Let's consider several examples of solving problems from Open bank assignments for

1 . Task B15 (# 26695)

On the segment.

1. The function is defined for all real values ​​of x

Obviously, these equations have no solutions, and the derivative is positive for all values ​​of x. Consequently, the function increases and takes its greatest value at the right end of the interval, that is, at x = 0.

Answer: 5.

2 . Task B15 (# 26702)

Find the largest function value on the segment.

1. ODZ functions title = "(! LANG: x (pi) / 2 + (pi) k, k (in) (bbZ)">!}

The derivative is equal to zero at, however, at these points it does not change sign:

Therefore, title = "(! LANG: 3 / (cos ^ 2 (x))> = 3">, значит, title="3 / (cos ^ 2 (x)) - 3> = 0">, то есть производная при всех допустимых значених х неотрицательна, следовательно, функция !} increases and takes the greatest value at the right end of the interval, at.

To make it obvious why the derivative does not change sign, we transform the expression for the derivative as follows:

Title = "(! LANG: y ^ (prime) = 3 / (cos ^ 2 (x)) - 3 = (3-3cos ^ 2 (x)) / (cos ^ 2 (x)) = (3sin ^ 2 (x)) / (cos ^ 2 (x)) = 3tg ^ 2 (x)> = 0">!}

Answer: 5.

3. Task B15 (# 26708)

Find the smallest value of the function on the segment.

1. ODZ function: title = "(! LANG: x (pi) / 2 + (pi) k, k (in) (bbZ)">!}

We place the roots of this equation on a trigonometric circle.

There are two numbers in between: and

Let's place the signs. To do this, we define the sign of the derivative at the point x = 0: ... When passing through the points and the derivative changes sign.

Let us represent the change of signs of the derivative of the function on the coordinate line:

Obviously, the point is a minimum point (at it the derivative changes sign from "-" to "+"), and to find the smallest value of the function on the segment, you need to compare the values ​​of the function at the minimum point and at the left end of the segment,.

The lesson on the topic "Using a derivative to find the largest and smallest values ​​of a continuous function on an interval" will consider relatively simple problems of finding the largest and smallest values ​​of a function over a given interval using the derivative.

Theme: Derivative

Lesson: Using the derivative to find the largest and smallest values ​​of a continuous function on an interval

In this lesson, we will consider more simple task, namely, the interval will be given, the continuous function at this interval. It is necessary to find out the largest and smallest value of the given functions on a given the interval.

No. 32.1 (b). Given:,. Let's draw a graph of the function (see Fig. 1).

Rice. 1. Graph of a function.

It is known that this function increases in the interval, which means that it also increases in the interval. So, if you find the value of the function at the points and, then the limits of change of this function, its largest and smallest value, will be known.

When the argument increases from to 8, the function increases from to.

Answer: ; .

№ 32.2 (a) Given: Find the largest and smallest values ​​of the function on a given interval.

Let's build a graph of this function (see Fig. 2).

If the argument changes in the interval, then the function increases from -2 to 2. If the argument increases from, then the function decreases from 2 to 0.

Rice. 2. Function graph.

Let's find the derivative.

, ... If, then this value also belongs to the specified segment. If, then. It is easy to check if it takes other values, the corresponding stationary points go beyond the specified segment. Let us compare the values ​​of the function at the ends of the segment and at the selected points at which the derivative is equal to zero. Find

;

Answer: ;.

So, the answer is received. The derivative in this case can be used, you can not use it, apply the properties of the function that were studied earlier. This is not always the case, sometimes the use of a derivative is the only method that allows you to solve such problems.

Given:,. Find the largest and smallest value of the function on a given segment.

If in the previous case it was possible to do without the derivative - we knew how the function behaves, then in this case the function is quite complex. Therefore, the technique that we mentioned in the previous task is fully applicable.

1. Find the derivative. Let's find the critical points, hence the critical points. From them we select those that belong to the given segment:. Let's compare the value of the function at the points,,. For this we find

Let us illustrate the result in the figure (see Fig. 3).

Rice. 3. Limits of change of function values

We see that if the argument changes from 0 to 2, the function changes from -3 to 4. The function does not change monotonically: it either increases or decreases.

Answer: ;.

So, three examples were used to demonstrate a general technique for finding the largest and smallest values ​​of a function on an interval, in this case, on a segment.

Algorithm for solving the problem of finding the largest and smallest values ​​of a function:

1. Find the derivative of the function.

2. Find the critical points of the function and select those points that are on a given segment.

3. Find the values ​​of the function at the ends of the segment and at the selected points.

4. Compare these values, and choose the largest and smallest.

Let's take another example.

Find the largest and smallest value of the function,.

Previously, the graph of this function was considered (see Fig. 4).

Rice. 4. Function graph.

In the interval, the range of this function is ... Point is the maximum point. At - the function increases, at - the function decreases. It can be seen from the drawing that, - does not exist.

So, in the lesson, we considered the problem of the largest and smallest function value, when the given interval is a segment; formulated an algorithm for solving such problems.

1. Algebra and the beginning of analysis, grade 10 (in two parts). Tutorial for educational institutions (profile level) ed. A.G. Mordkovich. -M .: Mnemosina, 2009.

2. Algebra and the beginning of analysis, grade 10 (in two parts). Problem book for educational institutions (profile level), ed. A.G. Mordkovich. -M .: Mnemosina, 2007.

3. Vilenkin N.Ya., Ivashev-Musatov O.S., Schwarzburd S.I. Algebra and calculus for grade 10 ( tutorial for students of schools and classes with in-depth study mathematics) .- M .: Education, 1996.

4. Galitsky M.L., Moshkovich M.M., Shvartsburd S.I. In-depth study of algebra and mathematical analysis.-M .: Education, 1997.

5. Collection of problems in mathematics for applicants to higher educational institutions (under the editorship of MI Skanavi) .- M.: Higher school, 1992.

6. Merzlyak A.G., Polonskiy VB, Yakir M.S. Algebraic simulator.-K .: A.S.K., 1997.

7. Zvavich L.I., Shlyapochnik L.Ya., Chinkina Algebra and the beginning of analysis. 8-11 grades: A manual for schools and classes with advanced study of mathematics (didactic materials) .- M .: Bustard, 2002.

8. Sahakyan S.M., Goldman A.M., Denisov D.V. Tasks in algebra and the principles of analysis (manual for students in grades 10-11 of general education institutions) .- M .: Education, 2003.

9. Karp A.P. Collection of problems in algebra and the principles of analysis: textbook. allowance for 10-11 grades with deepening study mathematics.-M .: Education, 2006.

10. Glazer G.I. History of mathematics at school. 9-10 grades (manual for teachers) .- M .: Education, 1983

Additional web resources

2. Portal Natural Sciences ().

Make at home

No. 46.16, 46.17 (c) (Algebra and the beginning of analysis, grade 10 (in two parts). Problem book for educational institutions (profile level) edited by A. G. Mordkovich. -M .: Mnemozina, 2007.)

The process of finding the smallest and largest value of a function on a segment resembles a fascinating flyby of an object (function graph) in a helicopter, firing at certain points from a long-range cannon and choosing from these points very special points for control shots. Points are chosen in a certain way and according to certain rules. What are the rules? We will talk about this further.

If the function y = f(x) is continuous on the segment [ a, b], then it reaches on this segment the smallest and highest values ... This can happen either in extremum points, or at the ends of the segment. Therefore, to find the smallest and maximum function values continuous on the segment [ a, b], you need to calculate its values ​​in all critical points and at the ends of the segment, and then choose the smallest and largest of them.

Let, for example, it is required to determine the largest value of the function f(x) on the segment [ a, b]. To do this, find all its critical points lying on [ a, b] .

Critical point is called the point at which function defined, and her derivative is either zero or does not exist. Then you should calculate the values ​​of the function at the critical points. And, finally, one should compare the values ​​of the function at critical points and at the ends of the segment ( f(a) and f(b)). The largest of these numbers will be the largest value of the function on the segment [a, b] .

The problems of finding smallest function values .

Looking for the smallest and largest values ​​of the function together

Example 1. Find the smallest and largest values ​​of a function on the segment [-1, 2] .

Solution. Find the derivative of this function. Let us equate the derivative to zero () and get two critical points: and. To find the smallest and largest values ​​of a function on a given segment, it is sufficient to calculate its values ​​at the ends of the segment and at a point, since the point does not belong to the segment [-1, 2]. These function values ​​are as follows:,,. It follows that smallest function value(in the graph below it is marked in red), equal to -7, is reached at the right end of the segment - at the point, and the greatest(also red on the graph), equal to 9, - at the critical point.

If a function is continuous in some interval and this interval is not a segment (but is, for example, an interval; the difference between an interval and a segment: the boundary points of the interval are not included in the interval, and the boundary points of the segment are included in the segment), then among the values ​​of the function it may not be be the smallest and the largest. So, for example, the function shown in the figure below is continuous at] -∞, + ∞ [and has no greatest value.

However, for any interval (closed, open, or infinite), the following property of continuous functions is true.

Example 4. Find the smallest and largest values ​​of a function on the segment [-1, 3] .

Solution. We find the derivative of this function as the derivative of the quotient:

.

We equate the derivative to zero, which gives us one critical point:. It belongs to the segment [-1, 3]. To find the smallest and largest values ​​of a function on a given segment, we find its values ​​at the ends of the segment and at the found critical point:

We compare these values. Conclusion: equal to -5/13, at point and the greatest value equal to 1 at the point.

We continue to search for the smallest and largest values ​​of the function together

There are teachers who, on the topic of finding the smallest and largest values ​​of a function, do not give students to solve examples more complicated than those just considered, that is, those in which the function is a polynomial or a fraction, the numerator and denominator of which are polynomials. But we will not limit ourselves to such examples, since among teachers there are those who like to make students think in full (table of derivatives). Therefore, the logarithm and trigonometric function will be used.

Example 6. Find the smallest and largest values ​​of a function on the segment .

Solution. Find the derivative of this function as derivative work :

We equate the derivative to zero, which gives one critical point:. It belongs to the segment. To find the smallest and largest values ​​of a function on a given segment, we find its values ​​at the ends of the segment and at the found critical point:

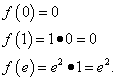
The result of all actions: function reaches its smallest value equal to 0 at the point and at the point and the greatest value equal to e², at the point.

Example 7. Find the smallest and largest values ​​of a function on the segment .

Solution. Find the derivative of this function:

Equating the derivative to zero:

The only critical point belongs to the line segment. To find the smallest and largest values ​​of a function on a given segment, we find its values ​​at the ends of the segment and at the found critical point:

Output: function reaches its smallest value equal to at the point and the greatest value, equal, at the point.

In applied extreme problems, finding the smallest (largest) values ​​of a function, as a rule, is reduced to finding a minimum (maximum). But the bigger practical interest have not the minima or maxima themselves, but those values ​​of the argument at which they are reached. When solving applied problems, an additional difficulty arises - the compilation of functions describing the phenomenon or process under consideration.

Example 8. A tank with a capacity of 4, which has the shape of a parallelepiped with a square base and is open at the top, must be fished out with tin. How big should the tank be to cover the least amount of material?

Solution. Let be x- side of the base, h- tank height, S- its surface area without a cover, V- its volume. The surface area of ​​the tank is expressed by the formula, i.e. is a function of two variables. To express S as a function of one variable, we will use what, whence. Substituting the found expression h into the formula for S:

Let us examine this function for an extremum. It is defined and differentiable everywhere in] 0, + ∞ [, and

.

Equate the derivative to zero () and find the critical point. In addition, for the derivative does not exist, but this value is not included in the domain of definition and therefore cannot be an extremum point. So, this is the only critical point. Let's check it for the presence of an extremum using the second sufficient criterion. Let's find the second derivative. When the second derivative is greater than zero (). Hence, at, the function reaches a minimum ... Since this minimum is the only extremum of this function, it is also its smallest value... So, the side of the base of the tank should be equal to 2 m, and its height.

Example 9. From paragraph A located on the railway line to point WITH at a distance from her l, cargo must be transported. The cost of transporting a weight unit per unit of distance by rail is equal, and by highway it is equal. To what point M the lines railroad a highway should be laid to transport cargo from A v WITH was the most economical (section AB the railway is assumed to be straight)?