Opće teoreme dinamike, tehnička mehanika. Opće teoreme dinamike. Dinamika materijalnog sistema i krutog tijela

Dom

Diferencijalne jednačine kretanja sistema.

Primjenjujemo drugi (osnovni) zakon dinamike, dobijamo Dobijamo sličan tip jednačine za bilo koju tačku u sistemu, tj. ukupno za sistem koji se razmatra biće n takvih jednačina (k= 1, 2….n). Ovaj sistem jednačina je

diferencijalne jednadžbe kretanja mehaničkog sistema u vektorskom obliku.

Projektovanjem jednakosti (2) na neke koordinatne ose dobijamo sistem diferencijalnih jednačina kretanja sistema u projekcijama na te ose.

Kao rezultat integracije sistema diferencijalnih jednačina (što je veoma teško), dobijamo zakone kretanja svake tačke sistema. Mnogo je zgodnije odrediti neke zbirne karakteristike kretanja cijelog sistema u cjelini i iz njih, ako je potrebno, pronaći odgovarajuće parametre kretanja pojedinih tačaka sistema.

Takve karakteristike su mjere kretanja sistema: impuls, ugaoni moment, kinetička energija.

Štaviše, svaka od ovih mjera za sistem je definirana kao zbir odgovarajućih mjera kretanja svih njegovih tačaka.

Shodno tome, uticaji na sistem se razmatraju ukupno (glavni vektor i glavni moment sila koje se primenjuju na sistem, količina rada itd.). Odnos između mjera kretanja sistema i mjera uticaja na njega izražava se pomoću opšte teoreme

sistemi materijalnih tačaka.

Opće teoreme dinamike sistema su posljedice sistema jednačina (2).

2) Masa sistema. Centar mase

Mehanički sistem je sistem materijalnih tačaka, od kojih svaka ima određenu masu i zauzima određenu poziciju u prostoru u datom trenutku vremena.

Radi praktičnosti rješavanja problema dinamike mehaničkih sistema, poželjno je imati neke generalizovane (tj. ukupne) karakteristike koje bi odražavale i masu sistema i njegovu „geometriju mase“, tj. lokacija u prostoru materijalnih tačaka sistema.

Masa sistema M jednaka je aritmetičkom zbiru masa svih tačaka ili tela koja čine sistem:

Centar mase mehaničkog sistema je geometrijska tačka C, čiji je poluprečnik vektor

gdje je radijus vektor tačaka koje formiraju sistem.

Mase tačaka mehaničkog sistema

Centar mase sistema nije materijalna tačka, već geometrijska. Možda se ne podudara ni sa jednom materijalnom tačkom sistema. Centar mase sistema karakteriše raspodelu masa u sistemu.

Teorema o kretanju centra mase mehaničkog sistema.

Teorema: Centar mase sistema se kreće kao materijalna tačka čija je masa jednaka masi čitavog sistema i na koju se primenjuju sve spoljne sile koje deluju na sistem.

Gdje je ubrzanje centra mase.

Glavni vektor vanjskih sila.

Projektovanjem obe strane jednačine na koordinatne ose, dobijamo:

gdje su ,, koordinate centra mase.

Iz teoreme o kretanju centra mase mogu se dobiti sljedeće važne posljedice koje izražavaju zakon održanja centra mase mehaničkog sistema.

Ako je geometrijski sistem svih vanjskih sila koje djeluju na sistem jednak 0 (), to znači da ili, tj. centar mase ovog sistema kreće se brzinom konstantnom po veličini i pravcu (drugim rečima, ravnomerno i pravolinijsko). U određenom slučaju, ako je prvo središte mase mirovalo () onda će ostati u mirovanju, tj. ().

Ako su vanjske sile koje djeluju na sistem takve da je zbir njihovih projekcija na neku osu (na primjer, os X jednaka 0, odnosno projekcija brzine centra mase sistema na ovu osu je konstantna vrijednost U konkretnom slučaju, ako u početnom trenutku, onda će u svakom narednom trenutku ta vrijednost ostati ista, pa se stoga koordinata centra mase sistema neće promijeniti, tj. = konst.

Teoreme o promjeni impulsa tačke i sistema

Definicija: količina kretanja materijalne tačke je vektorska veličina jednaka proizvodu mase tačke i njenog vektora brzine. Vektor se primjenjuje na pokretnu tačku.

Definicija: Količina kretanja mehaničkog sistema je vektor jednak geometrijskom zbiru količina kretanja svih tačaka sistema.

Vektor je slobodan vektor. Po pravilu su brzine svih tačaka sistema različite i stoga je direktno sabiranje vektora na desnoj strani jednakosti teško.

Koristimo formulu da odredimo centar mase mehaničkog sistema (1)

Ili možemo to napisati u formularu

Razlikovanjem oba dela izraza s obzirom na vreme dobijamo:

Upoređujući formule (4) i (5), nalazimo da je količina kretanja sistema jednaka proizvodu mase cijelog sistema i brzine njegovog centra mase.

Vektor je generalizovani vektor karakterističan za kretanje čitavog mehaničkog sistema. U opštem slučaju, kretanje sistema, njegov impuls se može posmatrati kao karakteristika translacionog dela kretanja sistema zajedno sa centrom mase. Ako, kada se sistem (tijelo) kreće, centar mase miruje, tada će količina kretanja biti jednaka 0. Na primjer, količina kretanja tijela koje rotira oko fiksne ose koja prolazi kroz njegovo središte mase.

Zapišimo drugi zakon dinamike za materijalnu tačku: uzimajući u obzir da dobijamo (7)

U svakom trenutku vremena, vremenski izvod impulsa tačke jednak je sili koja djeluje na tačku.

Ako se obje strane jednakosti (7) pomnože sa dt, tada dobivamo vektorsku količinu na desnoj strani ove jednakosti koja karakterizira djelovanje sile na tijelo u elementarnom vremenskom periodu dt ova veličina se naziva elementarni impuls sile, tj.

Teorema o kretanju centra masa. Diferencijalne jednačine kretanja mehaničkog sistema. Teorema o kretanju centra mase mehaničkog sistema. Zakon održanja kretanja centra masa.

Teorema o promjeni impulsa. Količina kretanja materijalne tačke. Elementarni impuls sile. Impuls sile u konačnom vremenskom periodu. Teorema o promjeni impulsa tačke u diferencijalnim i konačnim oblicima.

Količina kretanja mehaničkog sistema; njegov izraz kroz masu sistema i brzinu njegovog centra mase. Teorema o promjeni količine gibanja mehaničkog sistema u diferencijalnim i konačnim oblicima. Zakon održanja impulsa mehaničkog sistema.

Teorema o promjeni ugaonog momenta. Moment impulsa materijalne tačke u odnosu na centar i u odnosu na osu. Teorema o promjeni ugaonog momenta tačke.

Glavni moment impulsa ili kinetički moment mehaničkog sistema u odnosu na centar i u odnosu na osu. Kinetički moment rotacionog krutog tijela oko ose rotacije. Teorema o promjeni kinetičkog momenta mehaničkog sistema. Zakon održanja ugaonog momenta mehaničkog sistema.

Teorema o promjeni kinetičke energije. Kinetička energija materijalne tačke. Elementarni rad sile; analitički izraz elementarnog rada. Rad sile na konačnom pomaku tačke njene primjene. Rad gravitacije, elastične sile i sile gravitacije. Snaga. Teorema o promjeni kinetičke energije tačke.

Kinetička energija mehaničkog sistema. Kinetička energija krutog tijela pri translacijskom kretanju, pri rotaciji oko fiksne ose i pri ravnoparalelnom kretanju tijela. Teorema o promjeni kinetičke energije mehaničkog sistema. Zbir rada unutrašnjih sila u čvrstom tijelu jednak je nuli. Rad i snaga sila koje se primjenjuju na kruto tijelo koje rotira oko fiksne ose.

D'Alambertov princip. Princip mogućih pokreta. Sila inercije materijalne tačke. D'Alembertov princip za materijalnu tačku i mehanički sistem.

Predavanje 3. Opće teoreme dinamike

Dinamika sistema materijalnih tačaka je važna grana teorijske mehanike. Ovdje uglavnom razmatramo probleme o kretanju mehaničkih sistema (sistema materijalnih tačaka) sa konačnim brojem stupnjeva slobode – maksimalnim brojem nezavisnih parametara koji određuju položaj sistema. Glavni zadatak dinamike sistema je proučavanje zakona kretanja krutog tijela i mehaničkih sistema.

Najjednostavniji pristup proučavanju kretanja sistema koji se sastoji od N materijalnih tačaka, svodi se na razmatranje kretanja svake pojedinačne tačke sistema. U tom slučaju moraju se odrediti sve sile koje djeluju na svaku tačku sistema, uključujući sile interakcije između tačaka.

Određivanjem ubrzanja svake tačke u skladu sa drugim Newtonovim zakonom (1.2), dobijamo za svaku tačku tri skalarna diferencijalna zakona kretanja drugog reda, tj. 3 N diferencijalni zakoni kretanja za čitav sistem.

Da bi se pronašle jednačine kretanja mehaničkog sistema na osnovu datih sila i početnih uslova za svaku tačku sistema, moraju se integrisati rezultujući diferencijalni zakoni. Ovaj problem je težak čak iu slučaju dve materijalne tačke koje se kreću samo pod uticajem interakcijskih sila po zakonu univerzalne privlačnosti (problem dva tela), a izuzetno težak u slučaju tri tačke interakcije (problem tri tela). ).

Stoga je potrebno pronaći metode za rješavanje problema koje bi dovele do rješivih jednačina i dale predstavu o kretanju mehaničkog sistema. Opšte teoreme dinamike, kao posljedica diferencijalnih zakona kretanja, omogućavaju nam da izbjegnemo složenost koja nastaje prilikom integracije i dobijemo potrebne rezultate.

3. 1. Opće napomene

Brojaćemo tačke mehaničkog sistema indeksima i, j, k itd., koji prolaze kroz sve vrijednosti 1, 2, 3… N, Gdje N – broj bodova sistema. Fizičke veličine koje se odnose na k Tačke su označene istim indeksom kao i tačka. Na primjer, izrazite radijus vektor i brzinu, respektivno k th point.

Na svaku tačku sistema djeluju sile dva porijekla: prvo, sile čiji izvori leže izvan sistema, tzv. vanjski snage i određen ; drugo, sile iz drugih tačaka datog sistema, tzv interni snage i određen . Unutrašnje sile zadovoljavaju treći Newtonov zakon. Razmotrimo najjednostavnija svojstva unutrašnjih sila koje djeluju na cijeli mehanički sistem u bilo kojem stanju.

Prva nekretnina. Geometrijski zbir svih unutrašnjih sila sistema (glavni vektor unutrašnjih sila) jednak je nuli.

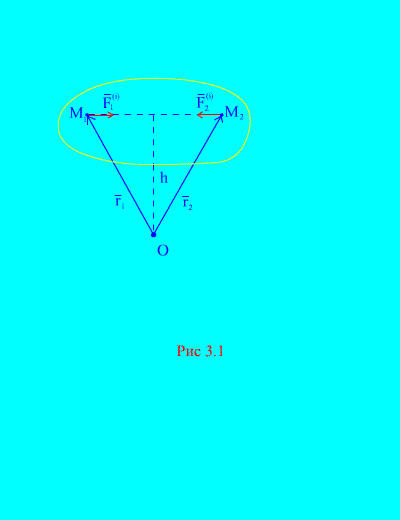
Zaista, ako uzmemo u obzir bilo koje dvije proizvoljne tačke sistema, na primjer i (Sl. 3.1), zatim za njih , jer sile akcije i reakcije su uvijek jednake po veličini, djelujući duž jedne linije djelovanja u suprotnom smjeru, koji povezuje tačke interakcije. Dakle, glavni vektor unutrašnjih sila čine parovi sila međudjelujućih tačaka

(3.1)

Druga nekretnina. Geometrijski zbir momenata svih unutrašnjih sila u odnosu na proizvoljnu tačku u prostoru jednak je nuli.

Razmotrimo sistem momenata sila u odnosu na tačku O(Sl. 3.1). Od (Sl. 3.1). to je jasno

,

jer obje sile imaju iste krakove i suprotne smjerove vektorskih momenata. Glavni moment unutrašnjih sila u odnosu na tačku O sastoji se od vektorske sume takvih izraza i jednaka je nuli. dakle,

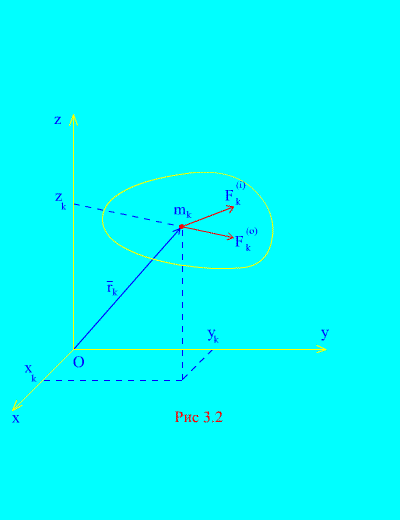
Neka vanjske i unutrašnje sile djeluju na mehanički sistem koji se sastoji od N bodova (Sl. 3.2). Ako se rezultanta vanjskih sila i rezultanta svih unutrašnjih sila primjenjuju na svaku tačku sistema, tada za bilo koju k U tački sistema, mogu se sastaviti diferencijalne jednačine kretanja. Biće ukupno takvih jednačina N:

i u projekcijama na fiksne koordinatne ose 3 N:

(3.4)

Vektorske jednačine (3.3) ili ekvivalentne skalarne jednačine (3.4) predstavljaju diferencijalne zakone kretanja materijalnih tačaka čitavog sistema. Ako se sve tačke kreću paralelno sa jednom ravninom ili jednom pravom linijom, tada će broj jednačina (3.4) u prvom slučaju biti 2 N, u drugom N.

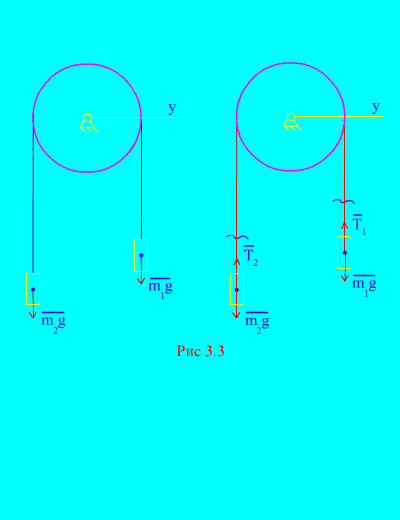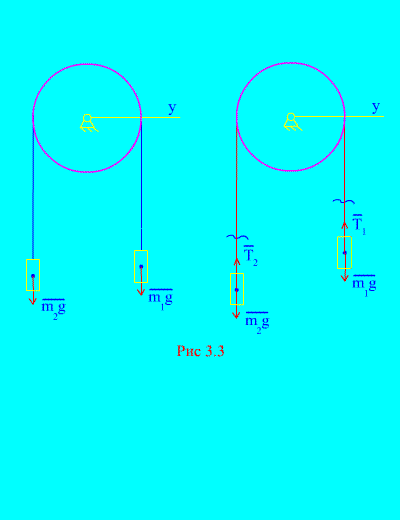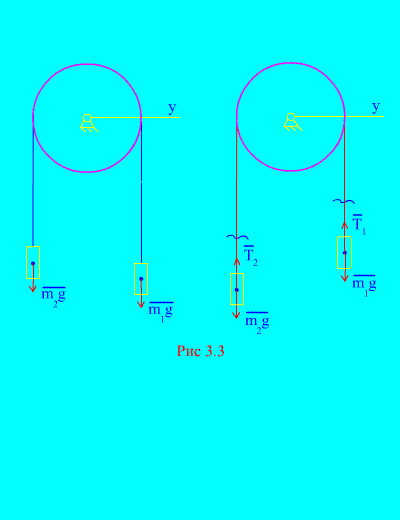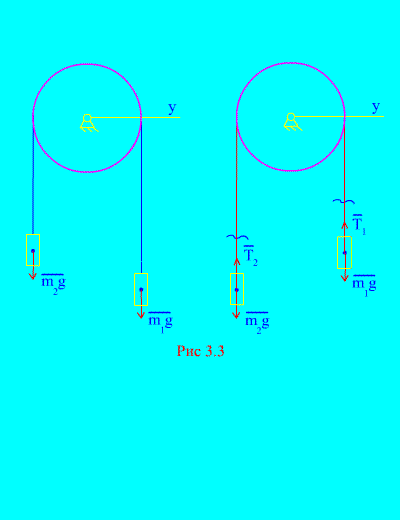
Primjer 1. Dvije mase su međusobno povezane nerastezljivim kablom prebačenim preko bloka (Sl. 3.3). Zanemarujući sile trenja, kao i masu bloka i sajle, određuju se zakon kretanja tereta i napetost kabla.

Rješenje. Sistem se sastoji od dva materijalna tijela (povezana nerastavljivim kablom) koja se kreću paralelno s istom osom X. Zapišimo diferencijalne zakone kretanja u projekcijama na osu X za svako telo.

Neka desna težina padne ubrzanjem, a zatim će lijeva težina rasti s ubrzanjem. Mentalno se oslobađamo veze (kabla) i zamjenjujemo je reakcijama i (Sl. 3.3). S obzirom da su tijela slobodna, nacrtajmo diferencijalne zakone kretanja u projekciji na osu X(što znači da su napetosti navoja unutrašnje sile, a težina opterećenja vanjske):

Pošto su i (tijela su povezana nerastezljivim užetom), dobijamo

Rješavanje ovih jednačina za ubrzanje i napetost kabla T, dobijamo

.

Imajte na umu da napetost u kablu nije jednaka sili gravitacije odgovarajućeg opterećenja.

3. 2. Teorema o kretanju centra masa

Poznato je da se kruto tijelo i mehanički sistem u ravni mogu kretati prilično složeno. Do prve teoreme o kretanju tijela i mehaničkog sistema može se doći na sljedeći način: baciti k.-l. predmet koji se sastoji od mnogo čvrstih tijela spojenih zajedno. Jasno je da će letjeti u paraboli. Ovo je otkriveno prilikom proučavanja kretanja tačke. Međutim, sada objekat nije tačka. Okreće se i njiše tokom leta oko nekog efektivnog centra koji se kreće po paraboli. Prva teorema o kretanju složenih objekata kaže da je određeni efektivni centar centar mase pokretnog objekta. Centar mase nije nužno lociran u samom tijelu;

Teorema. Centar mase mehaničkog sistema kreće se kao materijalna tačka sa masom jednakom masi celog sistema, na koju se primenjuju sve spoljašnje sile koje deluju na sistem.

Da bismo dokazali teoremu, prepisujemo diferencijalne zakone kretanja (3.3) u sljedećem obliku:

(3.5)

Gdje N – broj bodova sistema.

Hajde da saberemo jednačine pojam po član:

(A)

Položaj centra mase mehaničkog sistema u odnosu na odabrani koordinatni sistem određuje se formulom (2.1): Gdje M– masa sistema. Tada će biti zapisana lijeva strana jednakosti (a).

Prvi zbir na desnoj strani jednakosti (a) jednak je glavnom vektoru vanjskih sila, a posljednji, po svojstvu unutrašnjih sila, jednak je nuli. Tada će jednakost (a), uzimajući u obzir (b), biti prepisana

, (3.6)

one. proizvod mase sistema i ubrzanja centra njegove mase jednak je geometrijskom zbiru svih vanjskih sila koje djeluju na sistem.

Iz jednačine (3.6) proizilazi da unutrašnje sile ne utiču direktno na kretanje centra mase. Međutim, u nekim slučajevima oni su uzrok pojave vanjskih sila koje djeluju na sistem. Dakle, unutrašnje sile koje pokreću pogonske točkove automobila u rotaciju uzrokuju da vanjska sila prianjanja primijenjena na naplatak kotača djeluje na njega.

Primjer 2. Mehanizam, smješten u okomitoj ravnini, postavljen je na vodoravnu glatku ravninu i pričvršćen na nju šipkama čvrsto pričvršćenim na površinu TO I L (Sl. 3.4).

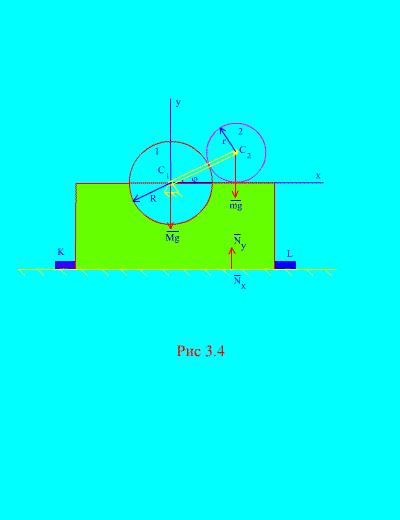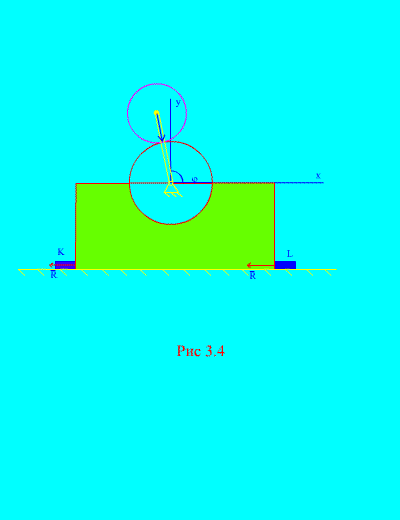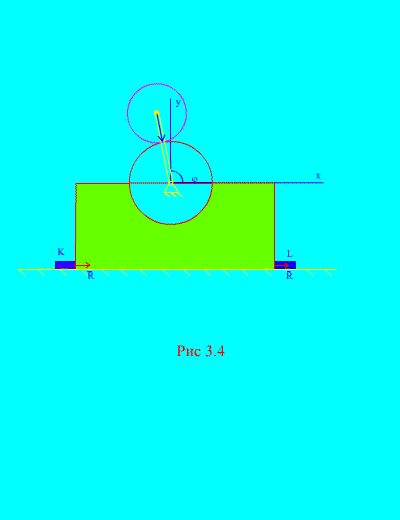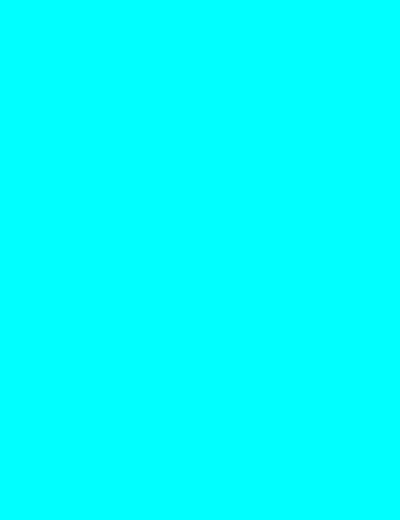
Radijus diska 1 R nepomičan. Disk 2 masa m i radijus r pričvršćena na polugu, dužina R+ r u tački C 2. Ručica se stalno okreće

ugaona brzina. U početnom trenutku, radilica je zauzela desni horizontalni položaj. Zanemarujući masu radilice, odredite maksimalne horizontalne i vertikalne sile koje djeluju na šipke ako je ukupna masa okvira i točka 1 jednaka M. Uzmite u obzir i ponašanje mehanizma u odsustvu šipki.

Rješenje. Sistem se sastoji od dvije mase ( N=2 ): fiksni disk 1 sa okvirom i pokretni disk 2. Usmjerite osovinu at kroz težište nepokretnog diska okomito prema gore, os X– duž horizontalne ravni.

Zapišimo teoremu o kretanju centra mase (3.6) u koordinatnom obliku

Vanjske sile ovog sistema su: težina okvira i fiksnog diska - Mg, težina diska u pokretu – mg, - ukupna horizontalna reakcija vijaka, - normalna ukupna reakcija ravnine. dakle,

Tada će zakoni kretanja (b) biti prepisani

Izračunajmo koordinate centra mase mehaničkog sistema:

; (G)

kao što se vidi iz (Sl. 3.4), , , (ugao poluge), . Zamjena ovih izraza u (d) i izračunavanje drugih izvoda s obzirom na vrijeme t iz , , to smo dobili

(e)

Zamjenom (c) i (e) u (b), nalazimo

Horizontalni pritisak koji djeluje na šipke je najveći i najmanji kada cos = 1 shodno tome, tj.

Pritisak mehanizma na horizontalnoj ravni ima najveću i najnižu vrijednost kada grijeh shodno tome, tj.

U stvari, prvi problem dinamike je riješen: prema poznatim jednačinama kretanja centra mase sistema (d), sile uključene u kretanje se obnavljaju.

U nedostatku rešetki K I L (Sl. 3.4), mehanizam može početi da poskakuje iznad horizontalne ravni. To će se dogoditi kada, tj. kada , slijedi da kutna brzina rotacije radilice, pri kojoj mehanizam odskače, mora zadovoljiti jednakost

.

3. 3. Zakon održanja kretanja centra masa

Ako je glavni vektor vanjskih sila koje djeluju na sistem jednak nuli, tj. , zatim od(3.6)slijedi da je ubrzanje centra mase nula, dakle, brzina centra mase je konstantna po veličini i smjeru. Ako, konkretno, u početnom trenutku centar mase miruje, onda miruje cijelo vrijeme dok je glavni vektor vanjskih sila jednak nuli.

Iz ove teoreme slijedi nekoliko posljedica.

· Unutrašnje sile same po sebi ne mogu promijeniti prirodu kretanja centra mase sistema.

· Ako je glavni vektor vanjskih sila koje djeluju na sistem jednak nuli, tada centar mase miruje ili se kreće ravnomjerno i pravolinijski.

· Ako je projekcija glavnog vektora vanjskih sila sistema na neku fiksnu osu jednaka nuli, tada se projekcija brzine centra mase sistema na ovu osu ne mijenja.

· Par sila primijenjen na kruto tijelo ne može promijeniti kretanje njegovog centra mase (može samo uzrokovati rotaciju tijela oko centra mase).

Razmotrimo primjer koji ilustruje zakon održanja kretanja centra mase.

Primjer 3. Dvije mase su povezane nerastavljivom niti bačenom kroz blok (Sl. 3.5), fiksiran na klin sa masom M. Klin se oslanja na glatku horizontalnu ravan. U početnom trenutku sistem je mirovao. Pronađite pomak klina duž ravnine kada se prvi teret spusti na visinu N. Zanemarite masu bloka i konca.

Rješenje. Vanjske sile koje djeluju na klin zajedno sa opterećenjima su gravitacija i Mg, kao i normalna reakcija glatke horizontalne površine N. Posljedično,

Pošto je u početnom trenutku sistem mirovao, imamo .

Izračunajmo koordinate centra mase sistema u i trenutno t 1 kada teret teži gće se spustiti na visinu H.

za sada:

,

Gdje , , X– koordinate centra mase tereta težine g, g i klina težine Mg.

Pretpostavimo da se klin u tom trenutku kreće u pozitivnom smjeru ose Ox po iznosu L, ako težina tereta padne na visinu N. Onda, za trenutak

jer tereti zajedno sa klinom će se pomeriti L udesno, a teret će se kretati prema gore duž klina. Budući da , onda nakon proračuna dobivamo

.

3.4. Količina pokreta sistema

3.4.1. Proračun impulsa sistema

Zamah materijalne tačke je vektorska veličina jednaka proizvodu mase tačke i njenog vektora brzine

Jedinica mjerenja momenta -

Impuls mehaničkog sistema je vektorski zbir impulsa pojedinih tačaka sistema, tj.

Gdje N – broj bodova sistema.

Zamah mehaničkog sistema može se izraziti u smislu mase sistema M i brzinu centra mase. stvarno,

one. Impuls sistema jednak je proizvodu mase čitavog sistema i brzine njegovog centra mase. Smjer je isti kao i smjer (Sl. 3.6)

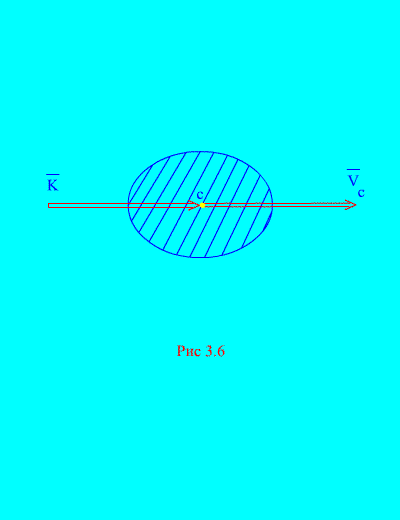
U projekcijama na pravougaone ose imamo

gdje su , , projekcije brzine centra mase sistema.

Evo M– masa mehaničkog sistema; se ne mijenja kada se sistem pomjeri.

Ovi rezultati su posebno pogodni za korištenje pri izračunavanju količina kretanja krutih tijela.

Iz formule (3.7) je jasno da ako se mehanički sistem kreće tako da njegovo središte mase ostaje nepomično, onda impuls sistema ostaje jednak nuli.

3.4.2. Elementarni impuls pune snage

Djelovanje sile na materijalnu tačku tokom vremena dt može se okarakterisati elementarnim impulsom. Ukupni impuls sile tokom vremena t, ili impuls sile, određen formulom

ili u projekcijama na koordinate osi

(3.8a)

Jedinica impulsa sile je .

3.4.3. Teorema o promjeni impulsa sistema

Neka spoljne i unutrašnje sile budu primenjene na tačke sistema. Tada za svaku tačku sistema možemo primijeniti diferencijalne zakone kretanja (3.3), imajući na umu da :

.

Sumirajući sve tačke sistema, dobijamo

Po svojstvu unutrašnjih sila i po definiciji imamo

(3.9)

Množenjem obje strane ove jednačine sa dt, dobijamo teoremu o promjeni impulsa u diferencijalnom obliku:

, (3.10)

one. diferencijalni impuls mehaničkog sistema jednak je vektorskom zbiru elementarnih impulsa svih vanjskih sila koje djeluju na tačke mehaničkog sistema.

Izračunavanje integrala obe strane (3.10) tokom vremena od 0 do t, dobijamo teoremu u konačnom ili integralnom obliku

(3.11)

U projekcijama na koordinatne ose ćemo imati

Promjena impulsa mehaničkog sistema tokom vremenat, jednak je vektorskom zbiru svih impulsa spoljnih sila koje deluju na tačke mehaničkog sistema u isto vreme.

Primjer 4. Težina opterećenja m spušta se niz nagnutu ravan iz stanja mirovanja pod uticajem sile F, proporcionalno vremenu: , gdje (Sl. 3.7). Koju će brzinu tijelo postići nakon toga t sekundi nakon početka kretanja, ako je koeficijent trenja klizanja tereta na kosoj ravni jednak f.

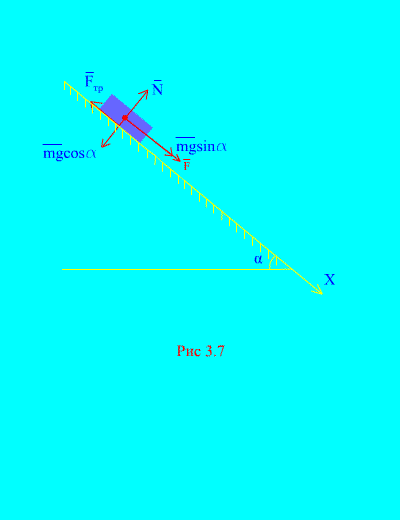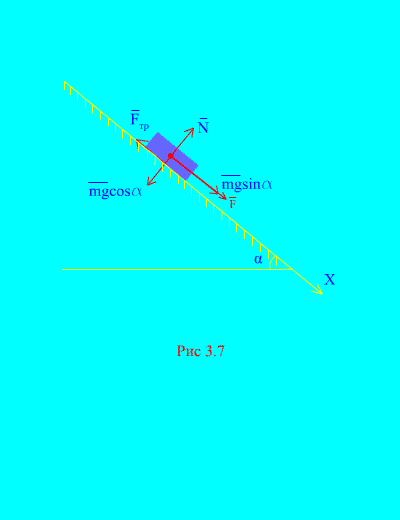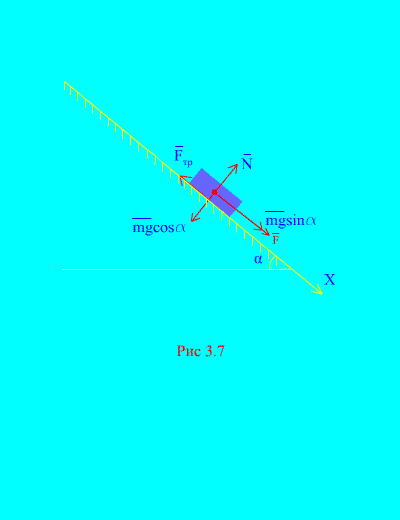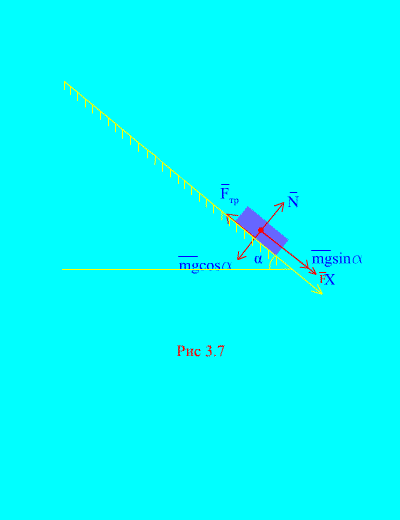
Rješenje. Hajde da opišemo sile koje se primenjuju na opterećenje: mg – sila gravitacije opterećenja, N je normalna reakcija ravnine, je sila trenja klizanja tereta na ravni, i . Smjer svih sila je prikazan u (Sl. 3.7).

Usmjerimo osu X duž nagnute ravni prema dolje. Napišimo teoremu o promjeni impulsa (3.11) u projekciji na osu X:

(A)

Prema stanju, jer u početnom trenutku je opterećenje bilo u mirovanju. Zbir projekcija impulsa svih sila na x osu je jednak

dakle,

,

.

3.4.4. Zakoni održanja impulsa

Zakoni održanja su dobijeni kao posebni slučajevi teoreme o promjeni impulsa. Moguća su dva posebna slučaja.

· Ako je vektorski zbir svih vanjskih sila primijenjenih na sistem jednak nuli, tj. , onda iz teoreme slijedi (3.9) , sta ,

one. ako je glavni vektor vanjskih sila sistema nula, tada je količina kretanja sistema konstantna po veličini i smjeru.

· Ako je projekcija glavnog vektora vanjskih sila na bilo koju koordinatnu osu jednaka nuli, na primjer Ox, tj. , tada je projekcija impulsa na ovu osu konstantna vrijednost.

Razmotrimo primjer primjene zakona održanja impulsa.

Primjer 5. Balističko klatno je tijelo s masom okačenom na dugačku nit (Sl. 3.8).

Metak mase koji se kreće brzinom V i udarivši u nepokretno tijelo, zaglavi se u njemu i tijelo odstupi. Kolika je bila brzina metka ako se tijelo podiglo na visinu h ?

Rješenje. Neka tijelo sa zaglavljenim metkom dobije brzinu. Zatim, koristeći zakon održanja količine kretanja tokom interakcije dva tijela, možemo pisati .

Brzina se može izračunati korištenjem zakona održanja mehaničke energije . Onda . Kao rezultat nalazimo

.

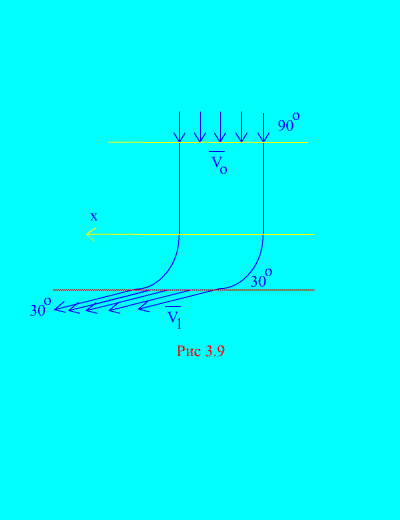
Primjer 6. Voda ulazi u stacionarni kanal (Sl. 3.9) varijabilni poprečni presjek sa brzinom pod uglom u odnosu na horizontalu; površina poprečnog presjeka kanala na ulazu; brzina vode na izlazu iz kanala čini ugao sa horizontom.

Odrediti horizontalnu komponentu reakcije koju voda ima na zidovima kanala. Gustina vode .

Rješenje. Odredit ćemo horizontalnu komponentu reakcije koju vrše zidovi kanala na vodu. Ova sila je jednaka po veličini i suprotnog predznaka od željene sile. Imamo, prema (3.11a),

. (A)

Izračunavamo masu zapremine tečnosti koja ulazi u kanal za vreme t:

Količina rAV 0 se zove druga masa - masa tekućine koja teče kroz bilo koji dio cijevi u jedinici vremena.

Ista količina vode izlazi iz kanala u isto vrijeme. Početna i konačna brzina su date u uslovu.

Izračunajmo desnu stranu jednakosti (a), koja određuje zbir projekcija na horizontalnu osu vanjskih sila primijenjenih na sistem (vodu). Jedina horizontalna sila je horizontalna komponenta rezultujuće reakcije zida Rx. Ova sila je konstantna tokom stabilnog kretanja vode. Zato

. (V)

Zamenivši (b) i (c) u (a), dobijamo

3.5. Kinetički moment sistema

3.5.1. Glavni moment impulsa sistema

Neka je radijus vektor tačke sa masom sistema u odnosu na neku tačku A, koja se zove centar (Sl. 3.10).

Moment momenta (kinetički moment) tačke u odnosu na centar A zove se vektor , određena formulom

. (3.12)

U ovom slučaju, vektor usmjeren okomito na ravan koja prolazi kroz centar A i vektor .

Moment momenta (kinetički moment) tačke u odnosu na osu naziva se projekcija momenta momenta momenta tačke na ovu osu u odnosu na bilo koji centar odabran na ovoj osi.

Glavni moment momenta (kinetički moment) sistema u odnosu na centar A naziva se količina

(3.13)

Glavni moment momenta (kinetički moment) sistema u odnosu na osu naziva se projekcija na ovu osu glavnog momenta momenta gibanja sistema u odnosu na bilo koji odabran na ovoj središnja os.

3.5.2. Kinetički moment rotirajućeg krutog tijela oko ose rotacije

Poravnajmo fiksnu tačku O tijelo koje leži na osi rotacije Oz, sa ishodištem koordinatnog sistema Ohooz, čije će se ose rotirati zajedno sa tijelom (Sl. 3.11). Neka je radijus vektor točke tijela u odnosu na početak koordinata njegova projekcija na os će biti označena sa , , . Projekcije vektora ugaone brzine tela na iste ose označavamo kao 0, 0, ().

TEOREMA MOMENTUMA (u diferencijalnom obliku).

1. Za tačku: derivacija impulsa tačke u odnosu na vrijeme jednaka je rezultanti sila primijenjenih na tačku:

ili u koordinatnom obliku:

2. Za sistem: derivacija impulsa sistema u odnosu na vrijeme jednaka je glavnom vektoru vanjskih sila sistema (vektorski zbir vanjskih sila primijenjenih na sistem):

ili u koordinatnom obliku:

TEOREMA O MOMENTU (teorema o momentu kretanja u konačnom obliku).

1. Za tačku: promjena impulsa tačke tokom konačnog vremenskog perioda jednaka je zbroju impulsa primijenjenih na tačku sile (ili rezultujućeg impulsa sila primijenjenih na tačku)

ili u koordinatnom obliku:

2. Za sistem: promjena impulsa sistema tokom konačnog vremenskog perioda jednaka je zbiru impulsa vanjskih sila:

ili u koordinatnom obliku:

Posljedice: u odsustvu vanjskih sila, količina kretanja sistema je konstantna vrijednost; ako su vanjske sile sistema okomite na određenu osu, tada je projekcija momenta na ovu osu konstantna vrijednost.

TEOREMA MOMENTUMA

1. Za tačku: Vremenska derivacija momenta zamaha tačke u odnosu na neki centar (os) jednaka je zbroju momenata sila primijenjenih na tačku u odnosu na isto središte (os):

2. Za sistem:

Vremenski izvod momenta količine kretanja sistema u odnosu na neki centar (os) jednak je zbiru momenata spoljnih sila sistema u odnosu na isto središte (os):

Posljedice: ako vanjske sile sistema ne daju moment u odnosu na dati centar (osu), tada je ugaoni moment sistema u odnosu na ovo središte (os) konstantna vrijednost.

Ako sile primijenjene na tačku ne proizvedu moment u odnosu na dati centar, tada je ugaoni moment tačke u odnosu na ovo središte konstantna vrijednost i tačka opisuje ravnu putanju.

TEOREMA KINETIČKE ENERGIJE

1. Za tačku: promjena kinetičke energije tačke pri njenom konačnom pomaku jednaka je radu aktivnih sila koje su na nju primijenjene (tangencijalne komponente reakcija neidealnih veza uključene su u broj aktivnih snage):

Za slučaj relativnog gibanja: promjena kinetičke energije tačke tokom relativnog kretanja jednaka je radu aktivnih sila koje su primijenjene na nju i prijenosnoj sili inercije (vidi "Posebni slučajevi integracije"):

2. Za sistem: promjena kinetičke energije sistema pri određenom pomaku njegovih tačaka jednaka je radu vanjskih aktivnih sila primijenjenih na njega i unutrašnjih sila primijenjenih na tačke sistema, udaljenost između koji se mijenja:

Ako je sistem nepromjenjiv (čvrsto tijelo), tada je ΣA i =0 i promjena kinetičke energije jednaka je radu samo vanjskih aktivnih sila.

TEOREMA O KRETANJU SREDIŠTA MASA MEHANIČKOG SISTEMA. Centar mase mehaničkog sistema kreće se kao tačka čija je masa jednaka masi cijelog sistema M=Σm i , na koju se primjenjuju sve vanjske sile sistema:

ili u koordinatnom obliku:

gdje je ubrzanje centra mase i njegova projekcija na kartezijanske koordinatne ose; vanjska sila i njene projekcije na kartezijanske koordinatne ose.

TEOREMA MOMENTA ZA SISTEM, IZRAŽENA U KROZ KRETANJE CENTRA MASA.

Promjena brzine centra mase sistema u konačnom vremenskom periodu jednaka je impulsu vanjskih sila sistema u istom vremenskom periodu, podijeljenom sa masom cijelog sistema.

Teorema o kretanju centra masa. Diferencijalne jednačine kretanja mehaničkog sistema. Teorema o kretanju centra mase mehaničkog sistema. Zakon održanja kretanja centra masa.

Teorema o promjeni impulsa. Količina kretanja materijalne tačke. Elementarni impuls sile. Impuls sile za konačan vremenski period i njegova projekcija na koordinatne ose. Teorema o promjeni impulsa materijalne tačke u diferencijalnim i konačnim oblicima.

Količina kretanja mehaničkog sistema; njegov izraz kroz masu sistema i brzinu njegovog centra mase. Teorema o promjeni količine gibanja mehaničkog sistema u diferencijalnim i konačnim oblicima. Zakon održanja impulsa mehaničke

(Koncept tijela i tačke promjenjive mase. Jednačina Meščerskog. Formula Ciolkovskog.)

Teorema o promjeni ugaonog momenta. Moment impulsa materijalne tačke u odnosu na centar i u odnosu na osu. Teorema o promjeni ugaonog momenta materijalne tačke. Centralna snaga. Očuvanje ugaonog momenta materijalne tačke u slučaju centralne sile. (Koncept sektorske brzine. Zakon površina.)

Glavni moment impulsa ili kinetički moment mehaničkog sistema u odnosu na centar i u odnosu na osu. Kinetički moment rotacionog krutog tijela oko ose rotacije. Teorema o promjeni kinetičkog momenta mehaničkog sistema. Zakon održanja ugaonog momenta mehaničkog sistema. (Teorema o promjeni kinetičkog momenta mehaničkog sistema u relativnom kretanju u odnosu na centar mase.)

Teorema o promjeni kinetičke energije. Kinetička energija materijalne tačke. Elementarni rad sile; analitički izraz elementarnog rada. Rad sile na konačnom pomaku tačke njene primjene. Rad gravitacije, elastične sile i sile gravitacije. Teorema o promjeni kinetičke energije materijalne točke u diferencijalnim i konačnim oblicima.

Kinetička energija mehaničkog sistema. Formule za izračunavanje kinetičke energije krutog tijela za vrijeme translacijskog kretanja, tijekom rotacije oko fiksne ose i u općenitom slučaju kretanja (posebno za vrijeme ravnoparalelnog kretanja). Teorema o promjeni kinetičke energije mehaničkog sistema u diferencijalnim i konačnim oblicima. Zbir rada unutrašnjih sila u čvrstom tijelu jednak je nuli. Rad i snaga sila koje se primjenjuju na kruto tijelo koje rotira oko fiksne ose.

Koncept polja sile. Potencijalno polje sila i funkcija sile. Izraz projekcija sile kroz funkciju sile. Površine jednakog potencijala. Rad sile na konačnom pomaku tačke u potencijalnom polju sila. Potencijalna energija. Primjeri polja potencijalnih sila: jednolično gravitacijsko polje i gravitacijsko polje. Zakon održanja mehaničke energije.

Dinamika krutog tijela. Diferencijalne jednadžbe translacijskog kretanja krutog tijela. Diferencijalna jednadžba za rotaciju krutog tijela oko fiksne ose. Fizičko klatno. Diferencijalne jednadžbe ravnog kretanja krutog tijela.

D'Alambertov princip. D'Alembertov princip za materijalnu tačku; inercijalna sila. D'Alembertov princip za mehanički sistem. Dovođenje sila inercije tačaka krutog tijela u centar; glavni vektor i glavni moment inercijskih sila.

(Određivanje dinamičkih reakcija ležajeva pri rotaciji krutog tijela oko fiksne ose. Slučaj kada je osa rotacije glavna centralna os inercije tijela.)

Princip mogućih kretanja i opšta jednačina dinamike. Veze nametnute mehaničkom sistemu. Moguća (ili virtuelna) kretanja materijalne tačke i mehaničkog sistema. Broj stepeni slobode sistema. Idealne veze. Princip mogućih pokreta. Opća jednadžba dinamike.

Jednačine kretanja sistema u generalizovanim koordinatama (Lagrangeove jednačine). Generalizirane koordinate sistema; generalizovane brzine. Izražavanje elementarnog rada u generaliziranim koordinatama. Generalizovane sile i njihov proračun; slučaj sila sa potencijalom. Uslovi za ravnotežu sistema u generalizovanim koordinatama. Diferencijalne jednačine kretanja sistema u generalizovanim koordinatama ili Lagranževe jednačine 2. vrste. Lagrangeove jednadžbe u slučaju potencijalnih sila; Lagrangeova funkcija (kinetički potencijal).

Koncept stabilnosti ravnoteže. Male slobodne vibracije mehaničkog sistema sa jednim stepenom slobode u blizini položaja stabilne ravnoteže sistema i njihova svojstva.

Elementi teorije udara. Fenomen uticaja. Udarna sila i udarni impuls. Djelovanje udarne sile na materijalnu tačku. Teorema o promjeni impulsa mehaničkog sistema pri udaru. Direktan centralni udar tijela na stacionarnu površinu; elastični i neelastični udari. Koeficijent povrata udara i njegovo eksperimentalno određivanje. Direktan centralni udar dva tijela. Carnotova teorema.

REFERENCE

Basic

Butenin N.V., Lunts Ya-L., Merkin D.R. Kurs teorijske mehanike. T. 1, 2. M., 1985. i prethodna izdanja.

Dobronravov V.V., Nikitin N.N. Kurs teorijske mehanike. M., 1983.

Staržinski V. M. Teorijska mehanika. M., 1980.

Targ S. M. Kratki kurs teorijske mehanike. M., 1986. i prethodna izdanja.

Yablonsky A. A., Nikiforova V. M. Kurs teorijske mehanike. Dio 1. M., 1984. i prethodna izdanja.

Yablonsky A. A. Kurs teorijske mehanike. Dio 2. M., 1984. i prethodna izdanja.

Meshchersky I. V. Zbirka zadataka iz teorijske mehanike. M., 1986. i prethodna izdanja.

Zbirka zadataka iz teorijske mehanike/Ur. K. S. Kolesnikova. M., 1983.

Dodatni

Bat M. I., Dzhanelidze G. Yu., Kelzon A. S. Teorijska mehanika u primjerima i problemima. Dijelovi 1, 2. M., 1984. i prethodna izdanja.

Zbirka zadataka iz teorijske mehanike/5razhnichen/so N. A., Kan V. L., Mintzberg B. L. i drugi M., 1987.

Novožilov I. V., Zatsepin M. F. Tipični računarski proračuni u teorijskoj mehanici. M., 1986,

Zbirka zadataka za nastavni rad iz teorijske mehanike / Ed. A. A. Yablonsky. M., 1985. i prethodna izdanja (sadrži primjere rješavanja problema).